题目内容
5.若f(x)=$\left\{\begin{array}{l}\frac{1}{a}-\frac{1}{x},\;\;0<\;x≤4\\ lnx-1,\;\;\;\;\;\;x>4\end{array}$在[$\frac{1}{2}$,2]上的最大值为2.(Ⅰ)求a的值;
(Ⅱ)求不等式f(x)<1的解集.
分析 (Ⅰ)易知f(x)=$\frac{1}{a}$-$\frac{1}{x}$在[$\frac{1}{2}$,2]上单调递增,从而可得f(2)=2,从而解得a;
(Ⅱ)由(I)知,分0<x≤4与x>4时分别解不等式f(x)<1,从而得到不等式的解集即可.
解答 解:(Ⅰ)由分段函数知,
f(x)=$\frac{1}{a}$-$\frac{1}{x}$在[$\frac{1}{2}$,2]上单调递增,
∴f(2)=2,
即$\frac{1}{a}$-$\frac{1}{2}$=2,
解得,a=$\frac{2}{5}$;
(Ⅱ)由(I)知,
当0<x≤4时,$f(x)=\frac{5}{2}-\frac{1}{x}<1$,
解得$0<x<\frac{2}{3}$;
当x>4时,
f(x)=lnx-1<1,
解得4<x<e2,
综上所述,不等式的解集为(0,$\frac{2}{3}$)∪(4,e2).
点评 本题考查了分段函数的应用,同时考查了分类讨论的思想应用及反比例函数与对数函数的性质应用,属于中档题.

练习册系列答案
相关题目
10.在坐标平面上,不等式组$\left\{\begin{array}{l}{y≥x-1}\\{y≤-3|x|+1}\end{array}\right.$所表示的平面区域的面积为( )
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | 2 |
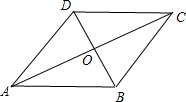 如图在菱形ABCD中,若AC=2,则$\overrightarrow{AB}$$•\overrightarrow{AC}$=2.
如图在菱形ABCD中,若AC=2,则$\overrightarrow{AB}$$•\overrightarrow{AC}$=2. 在数学研究性学习活动中,某小组要测量河对面A和B两个建筑物的距离,在河一侧取C、D两点,如图所示,测得CD=a,并且在C、D两点分别测得∠BAC=α,∠ACD=β,∠CDB=γ,∠BDA=?.
在数学研究性学习活动中,某小组要测量河对面A和B两个建筑物的距离,在河一侧取C、D两点,如图所示,测得CD=a,并且在C、D两点分别测得∠BAC=α,∠ACD=β,∠CDB=γ,∠BDA=?.