题目内容
设函数f (x)是(- ,+
,+ )上的减函数,又若a
)上的减函数,又若a R,则( )
R,则( )
| A.f (a)>f (2a) | B.f (a2)<f (a) |
| C.f (a2+a)<f (a) | D.f (a2+1) <f (a) |
D
解析试题分析:函数f (x)是(- ,+
,+ )上的减函数,且a2+1>a,所以f (a2+1) <f (a)
)上的减函数,且a2+1>a,所以f (a2+1) <f (a)
,故选D。
考点:本题主要考查函数的单调性,比较大小。
点评:简单题,利用函数的单调性,确定自变量大小,达到解题目的。

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
函数 在[0,2]上的最大值是7,则指数函数
在[0,2]上的最大值是7,则指数函数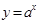 在[0,2]上的最大值与最小值的和为
在[0,2]上的最大值与最小值的和为
| A.6 | B.5 | C.3 | D.4 |
函数 的定义域是( )
的定义域是( )
A. | B. | C. | D.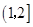 |
定义在 上的函数
上的函数 满足
满足 .当
.当 时,
时,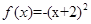 ,当
,当 时,
时, 。则
。则 ( )
( )
| A.335 | B.338 | C.1678 | D.2012 |
已知函数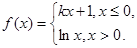 则下列关于函数
则下列关于函数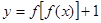 的零点个数的判断正确的是
的零点个数的判断正确的是
A.当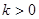 时,有3个零点;当 时,有3个零点;当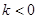 时,有2个零点 时,有2个零点 |
B.当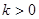 时,有4个零点;当 时,有4个零点;当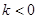 时,有1个零点 时,有1个零点 |
C.无论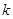 为何值,均有2个零点 为何值,均有2个零点 |
D.无论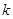 为何值,均有4个零点 为何值,均有4个零点 |
函数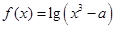 的定义域为[-1,1],且存在零点,则实数
的定义域为[-1,1],且存在零点,则实数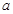 的取值范围是( )
的取值范围是( )
A.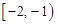 | B.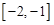 | C.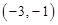 | D.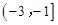 |
 在区间(
在区间( )的导函数
)的导函数 ,
, ,若在区间(
,若在区间( 恒成立,则称函数
恒成立,则称函数 在区间(
在区间( 若当实数
若当实数 满足
满足 时,函数
时,函数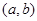 上为凸函数,则
上为凸函数,则 最大值 ( )
最大值 ( )


 是单调函数,则y=2ax+b的图象不可能是
是单调函数,则y=2ax+b的图象不可能是