题目内容
下列图形中,既是轴对称图形又是中心对称图形的是【 】

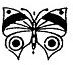
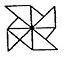
A B C D.
B
解析试题分析:对于A,C明显是轴对称图形,不是中心对称图形,对于D,可知为中心对称图像,对于B来说既可以看作是轴对称,也看做是中心对称,故选B.
考点:对称图形
点评:本试题考查了轴对称图形和中心对称图像的的概念,判断轴对称图像的关键是图像两部分沿着轴对称后重合,中心对称图形将原图形旋转180度后仍然重合。属于基础题。

练习册系列答案
相关题目
定义在R上的奇函数f(x),当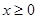 时,
时, ,则函数
,则函数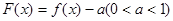 的所有零点之和为( )
的所有零点之和为( )
A.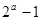 | B.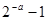 | C. | D.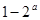 |
函数 的定义域为( )
的定义域为( )
A. | B. |
C. | D. 或 或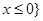 |
已知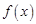 是
是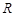 上的奇函数,且满足
上的奇函数,且满足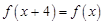 ,当
,当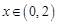 时,
时,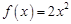 ,则
,则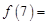 ( )
( )
| A.-2 | B.2 | C.4 | D.-4 |
设函数f (x)是(- ,+
,+ )上的减函数,又若a
)上的减函数,又若a R,则( )
R,则( )
| A.f (a)>f (2a) | B.f (a2)<f (a) |
| C.f (a2+a)<f (a) | D.f (a2+1) <f (a) |
函数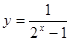 的值域是 ( )
的值域是 ( )
A.(-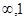 ) ) | B.(-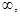 0) 0)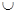 (0,+ (0,+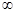 ) ) |
C.(-1,+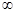 ) ) | D.(-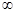 ,-1) ,-1)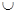 (0,+ (0,+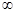 ) ) |
函数 的零点所在的区间是( )
的零点所在的区间是( )
A. | B. | C. | D. |
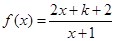 在
在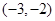 上是增函数,则二次函数
上是增函数,则二次函数 的图象可以为( ).
的图象可以为( ).
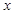
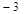
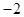
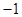
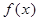
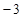
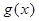
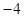
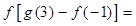 ( )
( )