题目内容
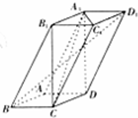 (2012•河北模拟)如图,四棱住ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.
(2012•河北模拟)如图,四棱住ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.(Ⅰ)求三棱柱C-A1B1C1的体积V;
(Ⅱ)求直线BD1与平面ADB1所成角的正弦值.
分析:(Ⅰ)由A1D⊥平面ABCD,可得A1D为两个底面的距离即三棱锥C-A1B1C1的高,再利用三棱锥C-A1B1C1的体积V=
S△A1B1C1×A1D计算公式即可得出;
(Ⅱ)通过建立如图所示的空间直角坐标系,先求出平面ADB1的法向量,利用BD1的方向向量与其法向量的夹角即可得出线面角.
| 1 |
| 3 |
(Ⅱ)通过建立如图所示的空间直角坐标系,先求出平面ADB1的法向量,利用BD1的方向向量与其法向量的夹角即可得出线面角.
解答:解:(Ⅰ)∵A1D⊥平面ABCD,∴A1D⊥AD,A1D即为两个底面的距离.
在Rt△A1DA中,∠A1DA=90°,AA1=2,AD=1,
由勾股定理得A1D=
=
.
又S△A1B1C1=
×1×1=
.
∴三棱锥C-A1B1C1的体积V=
S△A1B1C1×A1D=
×
×
=
;
(Ⅱ)建立如图所示的空间直角坐标系,
则D(0,0,0),A(1,0,0),B(1,1,0),
A1(0,0,
),B1(0,1,
),D1(-1,0,
),C1(-1,1,
).
∴
=(-2,-1,
),
=(1,0,0),
=(0,1,
).
设平面ADB1的法向量为
=(x,y,z),
则
,即
,
令z=1,则y=-
,x=0,∴
=(0,-
,1).
设直线BD1与平面ADB1所成角为θ,
则sinθ=|cos<
,
>|=
=
=
.
在Rt△A1DA中,∠A1DA=90°,AA1=2,AD=1,
由勾股定理得A1D=
| 22-12 |
| 3 |
又S△A1B1C1=
| 1 |
| 2 |
| 1 |
| 2 |
∴三棱锥C-A1B1C1的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 6 |
(Ⅱ)建立如图所示的空间直角坐标系,

则D(0,0,0),A(1,0,0),B(1,1,0),
A1(0,0,
| 3 |
| 3 |
| 3 |
| 3 |
∴
| BD1 |
| 3 |
| DA |
| DB1 |
| 3 |
设平面ADB1的法向量为
| n |
则
|
|
令z=1,则y=-
| 3 |
| n |
| 3 |
设直线BD1与平面ADB1所成角为θ,
则sinθ=|cos<
| n |
| BD1 |
|
| ||||
|
|
2
| ||||||||
|
| ||
| 4 |
点评:熟练掌握通过建立空间直角坐标系的方法求空间角、空间距离、线面垂直的判定与性质、三棱锥的体积计算公式是解题的关键.

练习册系列答案
相关题目
 (2012•河北模拟)设全集U=R,A={x|
(2012•河北模拟)设全集U=R,A={x| (2012•河北模拟)如图是一个程序框图,该程序框图输出的结果是
(2012•河北模拟)如图是一个程序框图,该程序框图输出的结果是 (2012•河北模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数f'(x)的部分图象如图所示,则函数f(x)的解析式为( )
(2012•河北模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数f'(x)的部分图象如图所示,则函数f(x)的解析式为( )