题目内容
【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-2x.
(1)求f(x)的解析式,并画出f(x)的图象;
(2)设g(x)=f(x)-k,利用图象讨论:当实数k为何值时,函数g(x)有一个零点?二个零点?三个零点?
【答案】(1) f(x)=![]() ,函数图象略.
,函数图象略.
(2)当k<-1或k>1时,有1个零点;当k=-1或k=1时,2个零点;
当-1<k<1时,3个零点.
【解析】
试题分析:(Ⅰ)先设x<0可得﹣x>0,则f(﹣x)=(﹣x)2﹣2(﹣x)=x2+2x,由函数f(x)为奇函数可得f(x)=﹣f(﹣x),可求,结合二次函数的图象可作出f(x)的图象
(II)由g(x)=f(x)﹣k=0可得f(x)=k,结合函数的图象可,要求g(x)=f(x)﹣k的零点个数,只要结合函数的图象,判断y=f(x)与y=k的交点个数
试题解析:
(Ⅰ)当x≥0时,f(x)=x2﹣2x.
设x<0可得﹣x>0,则f(﹣x)=(﹣x)2﹣2(﹣x)=x2+2x
∵函数f(x)为奇函数,则f(x)=﹣f(﹣x)=﹣x2﹣2x
∴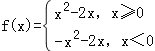 函数的图象如图所示
函数的图象如图所示
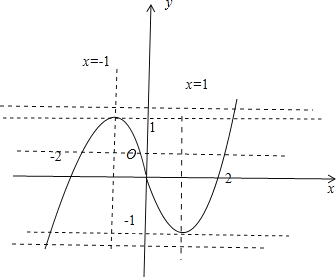
(II)由g(x)=f(x)﹣k=0可得f(x)=k
结合函数的图象可知
①当k<﹣1或k>1时,y=k与y=f(x)的图象有1个交点,即g(x)=f(x)﹣k有1个零点
②当k=﹣1或k=1时,y=k与y=f(x)有2个交点,即g(x)=f(x)﹣k有2个零点
③当﹣1<k<1时,y=k与y=f(x)有3个交点,即g(x)=f(x)﹣k有3个零点


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目