题目内容
已知复数z1满足：（1+2i）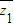
=4+3i，zn+1-zn=2+2i（n∈N+）．（1）求复数z1
（2）求满足|zn|≤13的最大正整数n．
【答案】分析：（1）设出复数，从而得到复数的共轭复数，把共轭复数代入所给的等式，得到关于a和b的等式，根据两个复数相等的充要条件，写出关于变量的方程组，得到结果．
（2）根据zn+1-zn=2+2i，仿写一系列这样的式子，一直到n=1，把所有的式子相加，利用叠加的方法，把出现的互为相反数的合并，这里的做法同求数列的通项一致，表示出模长，解不等式得到结果．
解答：解：（1）设z1=a+bi（a，b∈R），则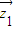
=a-bi
（1+2i）（a-bi）=4+3i
a+2b+（2a-b）i=4+3i
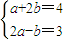
解得：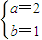
∴z1=2+i
（2）由zn+1-zn=2+2i（n∈N*）得：
z2-z1=2+2i
z3-z2=2+2i
z4-z3=2+2i
…
zn-zn-1=2+2i（n∈z，n≥2）
累加得zn-z1=2（n-1）+（n-1）i（n∈N*）
zn=2n+（2n-1）i（n∈N*）
|zn|=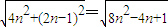
令|zn|≤13，即8n2-4n+1≤169
2n2-n-42≤0
∴
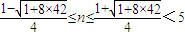
∴n的最大整数取值是4．
点评：本题考查复数的代数形式的运算，考查复数的模长，是一个综合题，解题的关键是写出要用模长的复数，这里采用叠加的方法，这是一个数列求通项常用的方法，更进一步理解知识是紧密联系的．
（2）根据zn+1-zn=2+2i，仿写一系列这样的式子，一直到n=1，把所有的式子相加，利用叠加的方法，把出现的互为相反数的合并，这里的做法同求数列的通项一致，表示出模长，解不等式得到结果．
解答：解：（1）设z1=a+bi（a，b∈R），则
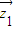=a-bi（1+2i）（a-bi）=4+3i
a+2b+（2a-b）i=4+3i
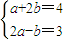
解得：
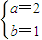
∴z1=2+i
（2）由zn+1-zn=2+2i（n∈N*）得：
z2-z1=2+2i
z3-z2=2+2i
z4-z3=2+2i
…
zn-zn-1=2+2i（n∈z，n≥2）
累加得zn-z1=2（n-1）+（n-1）i（n∈N*）
zn=2n+（2n-1）i（n∈N*）
|zn|=
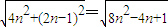
令|zn|≤13，即8n2-4n+1≤169
2n2-n-42≤0
∴
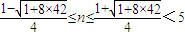
∴n的最大整数取值是4．
点评：本题考查复数的代数形式的运算，考查复数的模长，是一个综合题，解题的关键是写出要用模长的复数，这里采用叠加的方法，这是一个数列求通项常用的方法，更进一步理解知识是紧密联系的．
练习册系列答案
相关题目