题目内容
【题目】设{ an}为等比数列,{bn}为等差数列,且b1=0,cn=an+bn , 若{ cn}是1,1,2,…,求数列{ cn}的前10项和.
【答案】解:依题意:c1=a1+b1=1, ∵b1=0,
∴a1=1,
设 bn=b1+(n﹣1)d=(n﹣1)d(n∈N*),
an=a1qn﹣1=qn﹣1 , (n∈N*)
∵c2=a2+b2 ,
c3=a3+b3 ,
∴1=d+q,
2=2d+q2 ,
解得:q=0,d=1,或q=2,d=﹣1
∵q≠0,
∴q=2,d=﹣1.
∴an=2n﹣1(n∈N*),
bn=1﹣n (n∈N*),
∴c1+c2+…+c10=(a1+a2+…+a10)+(b1+b2+…+b10)
= ![]() +
+ ![]()
=210﹣1﹣10
=1024﹣46
=978
∴数列{ cn}的前10项和为978.
【解析】依题意:c1=a1﹣b1=1,由b1=0,知a1=1,设bn=(n﹣1)d,an=qn﹣1 , 由c2=a2+b2 , c3=a3+b3 , 知1=d+q,2=2d+q2 , 解得q=2,d=﹣1.所以a n=2 n﹣1(n∈N*),bn=1﹣n (n∈N*),由此能求出数列{ cn}的前10项和.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系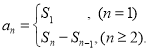 ).
).

练习册系列答案
相关题目