题目内容
(本小题满分14分)已知函数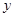 =
=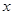 +
+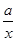 有如下性质:如果常数
有如下性质:如果常数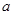 >0,那么该
>0,那么该
函数在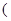 0,
0,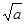
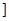 上是减函数,在
上是减函数,在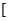
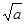 ,+∞
,+∞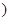 上是增函数.
上是增函数.
(1)如果函数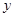 =
=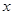 +
+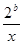 (
(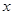 >0)的值域为
>0)的值域为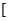 6,+∞
6,+∞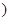 ,求
,求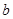 的值;
的值;
(2)研究函数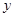 =
=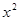 +
+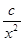 (常数
(常数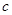 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;
(3)对函数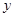 =
=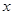 +
+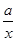 和
和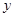 =
=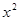 +
+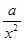 (常数
(常数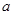 >0)作出推广,使它们都是你所推广的
>0)作出推广,使它们都是你所推广的
函数的特例.
(4)(理科生做)研究推广后的函数的单调性(只须写出结论,不必证明),并求函数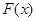 =
=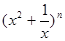 +
+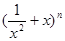 (
(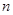 是正整数)在区间[
是正整数)在区间[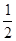 ,2]上的最大值和最小值(可利用你
,2]上的最大值和最小值(可利用你
的研究结论).
【答案】
解:(1)易知,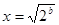 时,
时,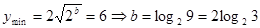 。
。
(2)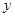 =
=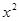 +
+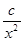 是偶函数。易知,该函数在
是偶函数。易知,该函数在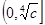 上是减函数,在
上是减函数,在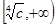 上是增函数;
上是增函数;
则该函数在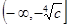 上是减函数,在
上是减函数,在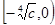 上是增函数。
上是增函数。
(3)推广:函数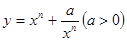 ,
,
当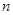 为奇数时,
为奇数时,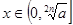 ,
,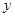 是减函数;
是减函数;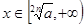 ,
,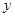 是增函数。
是增函数。
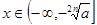 ,
,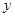 是增函数;
是增函数;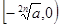 ,
,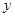 是减函数。
是减函数。
当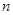 为偶数时,
为偶数时,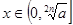 ,
,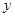 是减函数;
是减函数;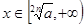 ,
,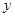 是增函数。
是增函数。 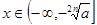 ,
,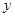 是减函数;
是减函数;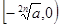 ,
,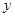 是增函数。
是增函数。
(4)(理科生做)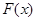 =
=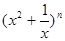 +
+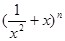
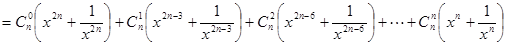
当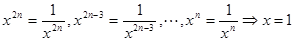 时,
时,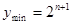 。
。
∴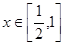 ,
,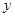 是减函数;
是减函数;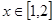 ,
,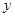 是增函数。
是增函数。
∵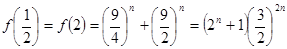
∴函数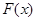 =
=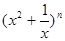 +
+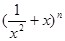 在区间[
在区间[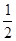 ,2]上的最大值为
,2]上的最大值为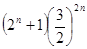 ,最小值为
,最小值为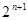 。
。
【解析】略

练习册系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)