题目内容
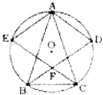 如图,AB=AC,∠ABC,∠ACB的平分线BD,CE分别交△ABC的外接圆D,E,且BD、CE相交于点F,则四边形AEFD是( )
如图,AB=AC,∠ABC,∠ACB的平分线BD,CE分别交△ABC的外接圆D,E,且BD、CE相交于点F,则四边形AEFD是( )| A、圆内接四边形 | B、菱形 | C、梯形 | D、矩形 |
考点:圆內接多边形的性质与判定
专题:直线与圆
分析:因为AB=AC,所以∠ABC=∠ACB;又因为BD、CE分别为∠ABC、∠ACB的平分线,所以∠ABD=∠DBC=∠ECB=∠ACE,因此AD=CD=BE=AE;然后判断出四边形AEFD是平行四边形,AD=AE,根据有一组邻边相等的平行四边形是菱形,可得四边形AEFD是菱形.
解答:解:∵AB=AC,
∴∠ABC=∠ACB;
又∵BD、CE分别为∠ABC、∠ACB的平分线,
∴∠ABD=∠DBC=∠ECB=∠ACE,
∴AD=CD=BE=AE;
又∵AE=CD,
∴∠ACE=∠DAC,
∴AD∥CE,
同理,可证AE∥BD,
∴四边形AEFD是平行四边形,AD=AE,
根据有一组邻边相等的平行四边形是菱形,
可得四边形AEFD是菱形.
故选:B.
∴∠ABC=∠ACB;
又∵BD、CE分别为∠ABC、∠ACB的平分线,
∴∠ABD=∠DBC=∠ECB=∠ACE,
∴AD=CD=BE=AE;
又∵AE=CD,
∴∠ACE=∠DAC,
∴AD∥CE,
同理,可证AE∥BD,
∴四边形AEFD是平行四边形,AD=AE,
根据有一组邻边相等的平行四边形是菱形,
可得四边形AEFD是菱形.
故选:B.
点评:此题主要考查了圆的内接多边形的性质的运用,考查了圆周角定理的推论,以及菱形的特征和判定,属于中档题.

练习册系列答案
相关题目
已知数列{an}是等比数列,且a2013+a2015=
dx.则a2014(a2012+2a2014+a2016)的值为( )
| ∫ | 2 0 |
| 8-x2 |
| A、(π+1)2 |
| B、4π2 |
| C、16π2 |
| D、(π+2)2 |
在极坐标系中,曲线ρ=4cos(θ-
)关于( )
| 5π |
| 6 |
A、直线θ=
| ||
B、直线θ=
| ||
C、点(2,
| ||
| D、极点中心对称 |
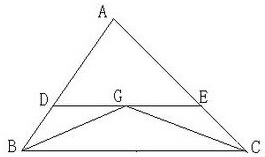
 如图,AE是圆O的切线,A是切点,AD与OE垂直,垂足是D.割线EC交圆D于B,C,且∠BDC=62°,∠DBE=108°,则∠OEC=
如图,AE是圆O的切线,A是切点,AD与OE垂直,垂足是D.割线EC交圆D于B,C,且∠BDC=62°,∠DBE=108°,则∠OEC=
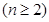 .如果
.如果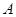 中元素
中元素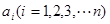 满足
满足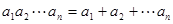 ,就称
,就称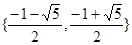 是“复活集”;
是“复活集”;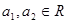 ,且
,且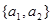 是“复活集”,则
是“复活集”,则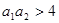 ;
;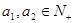 ,则
,则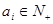 ,则“复合集”
,则“复合集”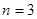 .
.