题目内容
5.新建的荆州中学拟模仿图甲建造一座体育馆,其设计方案侧面的外轮廓线如图乙所示:曲线AB是以点E为圆心的圆的一部分,其中E(0,t)(0<t≤8)单位:米);曲线BC是抛物线y=ax2+18(a<0)的一部分;CD⊥AD,且CD恰好等于圆E的半径.假定拟建体育馆的高OB=18米.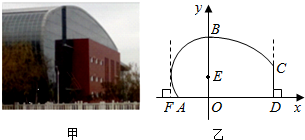
(Ⅰ)若要求CD=10米,AD=14米,求t与a的值;
(Ⅱ)若a=-$\frac{1}{36}$,将AD的长表示为点E的纵坐标t的函数f(t),并求AD的最大值.并求f(t)的最大值.(参考公式:若f(x)=$\sqrt{c-x}$,则f′(x)=-$\frac{1}{2\sqrt{c-x}}$,其中c为常数)
分析 (1)由题意可求得t=OB-EB=OB-CD=18-10=8,从而写出圆E的方程为x2+(y-8)2=100;从而求得C(8,10)在抛物线y=ax2+18上,从而求a;
(2)化简圆E的方程为x2+(y-t)2=(18-t)2,从而写出A(-$\sqrt{324-36t}$,0);即OA=6$\sqrt{9-t}$;再求出OD=6$\sqrt{t}$;从而得到f(t)=6$\sqrt{9-t}$+6$\sqrt{t}$(0<t≤8);求导
f′(t)=6($\frac{-1}{2\sqrt{9-t}}$+$\frac{1}{2\sqrt{t}}$)=3-$\frac{\sqrt{9-t}-\sqrt{t}}{\sqrt{9-t}\sqrt{t}}$;从而判断函数的单调性,从而求最大值.
解答 解:(1)由已知有,
t=OB-EB=OB-CD=18-10=8,
∴圆E的方程为x2+(y-8)2=100;
令y=0得A(-6,0),又AD=14,
∴OD=8,
即C(8,10)在抛物线y=ax2+18上,
∴a=-$\frac{1}{8}$;
(2)由题意得,CD=18-t,
∴圆E的方程为x2+(y-t)2=(18-t)2
令y=0得x2=324-36t,
∴A(-$\sqrt{324-36t}$,0);
∴OA=6$\sqrt{9-t}$;
由18-t=-$\frac{{x}^{2}}{36}$+18得x2=36t;
∴OD=6$\sqrt{t}$;
又AD=AO+OD=6$\sqrt{9-t}$+6$\sqrt{t}$;
∴f(t)=6$\sqrt{9-t}$+6$\sqrt{t}$(0<t≤8);
f′(t)=6($\frac{-1}{2\sqrt{9-t}}$+$\frac{1}{2\sqrt{t}}$)=3-$\frac{\sqrt{9-t}-\sqrt{t}}{\sqrt{9-t}\sqrt{t}}$;
令f′(t)=0得t=$\frac{9}{2}$,
当0<t<$\frac{9}{2}$时,f′(t)>0,f(t)单调递增;
当$\frac{9}{2}$<t≤8时,f′(t)<0,f(t)单调递减;
故t=$\frac{9}{2}$时,fmax(t)=18$\sqrt{2}$.
点评 本题考查了函数在实际问题中的应用,同时考查了导数的综合应用,属于难题.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |