题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的最小值;
的最小值;
(3)若![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)函数![]() 的单调减区间是
的单调减区间是![]() ,增区间是
,增区间是![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据解析式求出g(x)的定义域和g′(x),再求出临界点,求出g′(x)<0和g′(x)>0对应的解集,再表示成区间的形式,即所求的单调区间;
(2)先求出f(x)的定义域和f′(x),把条件转化为f′(x)≤0在(1,+∞)上恒成立,再对f′(x)进行配方,求出在x∈(1,+∞)的最大值,再令f′(x)max≤0求解;
(3)先把条件等价于“当x∈[e,e2]时,有f(x)min≤f′(x)max+a”,由(2)得f′(x)max,并把它代入进行整理,再求f′(x)在[e,e2]上的最小值,结合(2)求出的a的范围对a进行讨论:![]() 和
和![]() ,分别求出f′(x)在[e,e2]上的单调性,再求出最小值或值域,代入不等式再与a的范围进行比较.
,分别求出f′(x)在[e,e2]上的单调性,再求出最小值或值域,代入不等式再与a的范围进行比较.
由已知函数![]() 的定义域均为
的定义域均为![]() ,且
,且![]()
(1)函数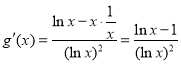 ,则
,则![]() ,
,
当![]() 且
且![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以函数![]() 的单调减区间是
的单调减区间是![]() ,增区间是
,增区间是![]() ;
;
(2)因![]() 在
在![]() 上为减函数,故
上为减函数,故![]() 在
在![]() 上恒成立,
上恒成立,
所以当![]() 时,
时,![]() ,
,
又![]() ,
,
故当![]() ,即
,即![]() 时,
时,![]() ,
,
所以![]() 于是
于是![]() ,故
,故![]() 的最小值为
的最小值为![]() ;
;
(3)命题“若![]() 使
使![]() 成立”等价于:
成立”等价于:
“当![]() 时,有
时,有![]() ”,
”,
由(2),当![]() 时,
时,![]() ,∴
,∴![]() ,
,
问题等价于:“当![]() 时,有
时,有![]() ”,
”,
①当![]() 时,由(2),
时,由(2),![]() 在
在![]() 上为减函数,
上为减函数,
则![]() ,故
,故![]() .
.
②当![]() 时,由于
时,由于![]() 在
在![]() 上为增函数,
上为增函数,
故![]() 的值域为
的值域为![]() ,即
,即![]() .
.
由![]() 的单调性和值域知,
的单调性和值域知,![]() 唯一
唯一![]() ,使
,使![]() ,且满足:
,且满足:
当![]() 时,
时,![]() ,
,![]() 为减函数;当
为减函数;当![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;
所以,![]() ,
,![]() .
.
所以,![]() ,与
,与![]() 矛盾,不合题意.
矛盾,不合题意.
综上,得![]() .
.

练习册系列答案
相关题目