题目内容
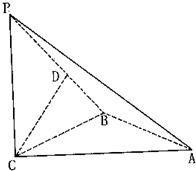 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.(1)求证:AB⊥平面PCB;
(2)求异面直线AP与BC所成角的大小.
分析:(1)由线面垂直的性质可得PC⊥AB,CD⊥AB,从而证明AB⊥平面PCB.
(2)过点A作AF∥BC,且AF=BC,∠PAF为异面直线PA与BC所成的角,直角三角形中利用边角关系求得所求角的
正切值,即得所求角的大小.
(2)过点A作AF∥BC,且AF=BC,∠PAF为异面直线PA与BC所成的角,直角三角形中利用边角关系求得所求角的
正切值,即得所求角的大小.
解答: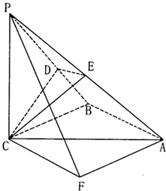 解:(1)∵PC⊥平面ABC,AB?平面ABC,∴PC⊥AB.
解:(1)∵PC⊥平面ABC,AB?平面ABC,∴PC⊥AB.
∵CD⊥平面PAB,AB?平面PAB,∴CD⊥AB.
又PC∩CD=C,∴AB⊥平面PCB.
(2)过点A作AF∥BC,且AF=BC,连接PF,CF.
则∠PAF为异面直线PA与BC所成的角.由(1)可得AB⊥BC,
∴CF⊥AF. 由三垂线定理,得PF⊥AF.
则AF=CF=
,PF=
=
.
在Rt△PFA中,tan∠PAF=
=
=
,∴∠PAF=
,
∴异面直线PA与BC所成的角为
.
 解:(1)∵PC⊥平面ABC,AB?平面ABC,∴PC⊥AB.
解:(1)∵PC⊥平面ABC,AB?平面ABC,∴PC⊥AB.∵CD⊥平面PAB,AB?平面PAB,∴CD⊥AB.
又PC∩CD=C,∴AB⊥平面PCB.
(2)过点A作AF∥BC,且AF=BC,连接PF,CF.
则∠PAF为异面直线PA与BC所成的角.由(1)可得AB⊥BC,
∴CF⊥AF. 由三垂线定理,得PF⊥AF.
则AF=CF=
| 2 |
| PC2+CF2 |
| 6 |
在Rt△PFA中,tan∠PAF=
| PF |
| AF |
| ||
|
| 3 |
| π |
| 3 |
∴异面直线PA与BC所成的角为
| π |
| 3 |
点评:本题考查证明线面垂直的方法,求异面直线所成的角,找出异面直线所成的角是解题的关键.

练习册系列答案
相关题目
 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB (2006•石景山区一模)如图,三棱锥P-ABC中,
(2006•石景山区一模)如图,三棱锥P-ABC中, (2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2
(2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2 (2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为
(2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为 如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,
如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,