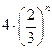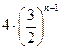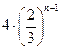题目内容
已知等比数列的前3项和为168,a2-a5=42,求a5,a7的等比中项.
a5,a7的等比中项是±3.
利用已知条件,列出关于首项a1和公比q的方程组,求出a1和q后,问题便得以解决.
设该等比数列的首项为a1,公比为q,由已知得

即
∵1-q3=(1-q)(1+q+q2),
∴由①②可得q(1-q)=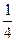 .
.
∴q=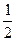 .此时a1=
.此时a1= =96.
=96.
若G是a5,a7的等比中项,则应有G2=a5·a7=a12·q10=962×(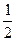 )10=9.
)10=9.
∴a5,a7的等比中项是±3.
设该等比数列的首项为a1,公比为q,由已知得

即

∵1-q3=(1-q)(1+q+q2),
∴由①②可得q(1-q)=
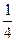 .
.∴q=
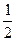 .此时a1=
.此时a1= =96.
=96.若G是a5,a7的等比中项,则应有G2=a5·a7=a12·q10=962×(
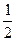 )10=9.
)10=9.∴a5,a7的等比中项是±3.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
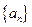 的前
的前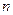 和为
和为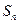 ,首项
,首项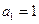 ,公比
,公比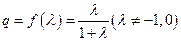
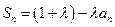 ;
;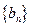 满足:
满足: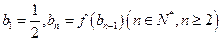 ,求数列
,求数列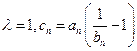 ,数列
,数列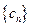 的前
的前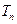 ,求证:当
,求证:当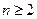 时,
时,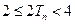 。
。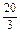 ,求{an}的通项公式.
,求{an}的通项公式.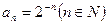 ,从数列
,从数列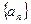 中取出部分项,按原来的顺序组成一个各项和为
中取出部分项,按原来的顺序组成一个各项和为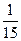 的无穷等比数列
的无穷等比数列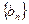 ,则
,则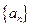 的前
的前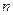 项和
项和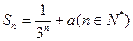 ,且
,且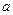 是常数,则此无穷等比数列各项的和等于 (用数值作答).
是常数,则此无穷等比数列各项的和等于 (用数值作答).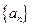 的前三项依次为
的前三项依次为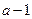 ,
,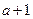 ,
,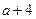 ,则
,则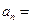 ( )
( )