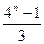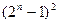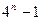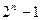题目内容
设等比数列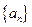 的前
的前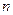 和为
和为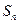 ,首项
,首项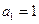 ,公比
,公比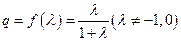
(1)证明: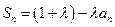 ;
;
(2)若数列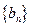 满足:
满足: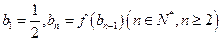 ,求数列
,求数列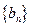 的通项公式;
的通项公式;
(3)记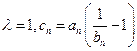 ,数列
,数列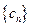 的前
的前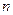 和为
和为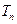 ,求证:当
,求证:当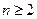 时,
时,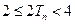 。
。
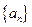 的前
的前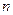 和为
和为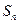 ,首项
,首项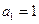 ,公比
,公比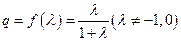
(1)证明:
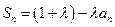 ;
;(2)若数列
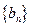 满足:
满足: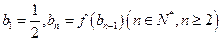 ,求数列
,求数列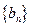 的通项公式;
的通项公式;(3)记
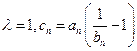 ,数列
,数列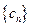 的前
的前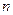 和为
和为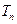 ,求证:当
,求证:当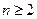 时,
时,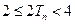 。
。(1)
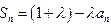 (2)
(2)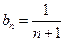
(1)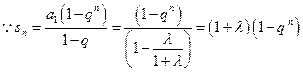 ,
,
又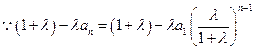 ,
,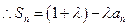
(2)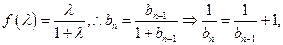 即
即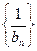 是首项为
是首项为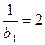 ,
,
公差为1的等差数列
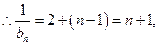 即
即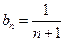
(3)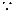 当
当 时,
时,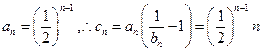 ,
,
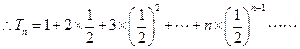 ①,
①,
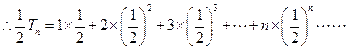 ②由①-②得
②由①-②得
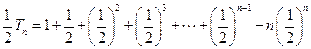 =
=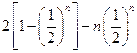 ,
,
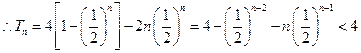 ,又
,又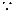 数列
数列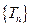 是单调递增的,
是单调递增的,
故当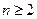 时,
时,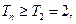 即当
即当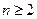 时,
时,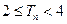
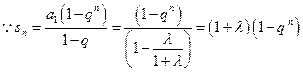 ,
,又
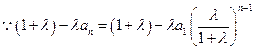 ,
,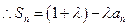
(2)
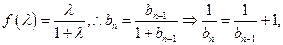 即
即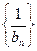 是首项为
是首项为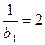 ,
,公差为1的等差数列
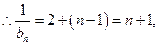 即
即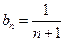
(3)
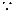 当
当 时,
时,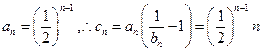 ,
,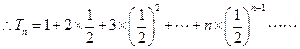 ①,
①,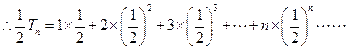 ②由①-②得
②由①-②得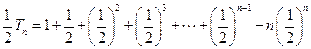 =
=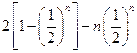 ,
,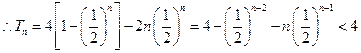 ,又
,又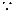 数列
数列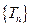 是单调递增的,
是单调递增的,故当
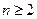 时,
时,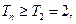 即当
即当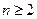 时,
时,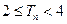

练习册系列答案
相关题目
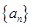 的各项均为正数,前四项之积等于64,那么
的各项均为正数,前四项之积等于64,那么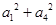 的最小值等于 。
的最小值等于 。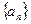 前
前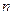 项之和为
项之和为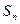 ,
, 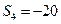 ,
,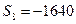 ,求
,求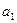 和
和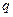
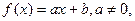
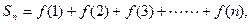 若
若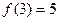 ,且
,且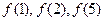 成等比数列,求
成等比数列,求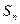
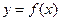 的图象经过坐标原点,其导函数为
的图象经过坐标原点,其导函数为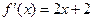 ,数列
,数列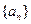 的首项
的首项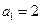 ,点
,点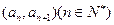 均在函数
均在函数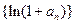 是公比为2的等比数列.
是公比为2的等比数列.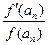 ,求数列
,求数列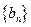 的前项和
的前项和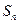 .
.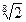
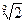
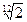
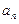 }中,若
}中,若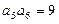 ,则
,则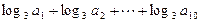 =( )
=( )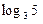
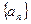 中,已知对任意自然数
中,已知对任意自然数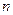 ,
,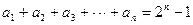 ,则
,则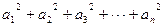 等于 ( )
等于 ( )