题目内容
已知{an}为等比数列,a3=2,a2+a4=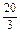 ,求{an}的通项公式.
,求{an}的通项公式.
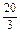 ,求{an}的通项公式.
,求{an}的通项公式.an=2×33-n或an=2×3n-3.
方法一 设等比数列{an}的公比为q,则q≠0,
a2=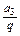 =
=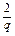 ,a4=a3q=2q,
,a4=a3q=2q,
∴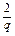 +2q=
+2q=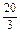 .
.
解得q1=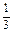 ,q2=3.
,q2=3.
①当q=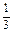 时,a1=18,
时,a1=18,
∴an=18×(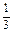 )n-1=
)n-1= =2×33-n.
=2×33-n.
②当q=3时,a1=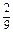 ,
,
∴an=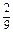 ×3n-1=2×3n-3.
×3n-1=2×3n-3.
∴an=2×33-n或an=2×3n-3.
方法二 由a3=2,得a2a4=4,
又a2+a4=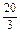 ,
,
则a2,a4为方程x2-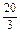 x+4=0的两根,
x+4=0的两根,
解得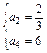 或
或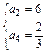 .
.
①当a2=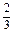 时,q=3,an=a3·qn-3=2×3n-3.
时,q=3,an=a3·qn-3=2×3n-3.
②当a2=6时,q=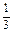 ,an=2×33-n
,an=2×33-n
∴an=2×3n-3或an=2×33-n.
a2=
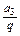 =
=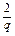 ,a4=a3q=2q,
,a4=a3q=2q,∴
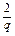 +2q=
+2q=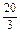 .
.解得q1=
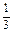 ,q2=3.
,q2=3.①当q=
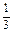 时,a1=18,
时,a1=18,∴an=18×(
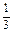 )n-1=
)n-1= =2×33-n.
=2×33-n.②当q=3时,a1=
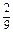 ,
,∴an=
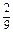 ×3n-1=2×3n-3.
×3n-1=2×3n-3.∴an=2×33-n或an=2×3n-3.
方法二 由a3=2,得a2a4=4,
又a2+a4=
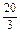 ,
,则a2,a4为方程x2-
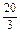 x+4=0的两根,
x+4=0的两根,解得
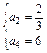 或
或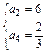 .
.①当a2=
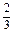 时,q=3,an=a3·qn-3=2×3n-3.
时,q=3,an=a3·qn-3=2×3n-3.②当a2=6时,q=
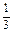 ,an=2×33-n
,an=2×33-n∴an=2×3n-3或an=2×33-n.

练习册系列答案
相关题目
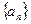 前
前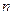 项之和为
项之和为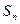 ,
, 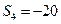 ,
,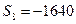 ,求
,求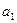 和
和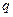
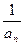 };(6){an+3}中,等比数列的个数是( )
};(6){an+3}中,等比数列的个数是( )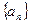 为等比数列,
为等比数列,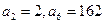 ,则
,则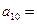
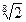
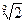
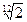
 成等比数列,则
成等比数列,则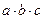 的值为_____________
的值为_____________