题目内容
4．若a=${log}_{\sqrt{2}}$$\frac{1}{\sqrt{3}}$，b=${log}_{\sqrt{2}}\frac{1}{\sqrt{2}}$，c=-2，则a、b、c的大小关系是（ ）| A． | a＞b＞c | B． | b＞c＞a | C． | b＞a＞c | D． | c＞b＞a |
分析 直接利用对数的运算法则比较a、b的大小，然后比较a、c的大小即可．
解答 解：因为$\frac{1}{\sqrt{3}}＜\frac{1}{\sqrt{2}}$，所以a=${log}_{\sqrt{2}}$$\frac{1}{\sqrt{3}}$＜b=${log}_{\sqrt{2}}\frac{1}{\sqrt{2}}$=-1，
又a=${log}_{\sqrt{2}}$$\frac{1}{\sqrt{3}}$＞${log}_{\sqrt{2}}\frac{1}{2}=-2$=c，
所以b＞a＞c．
故选：C．
点评 本题考查对数值的大小比较，对数的简单性质的应用，考查计算能力．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
14．某教辅集团进年要研究出版多种一轮用书，其中有A，B两种已经投入使用，经一学年使用过后，教辅团队为了调查书的质量与社会反响，特地选择某校高三的4个班进行调查，从各班抽取的样本人数如表：
（1）从10人中随机抽取2人，求这2人恰好来自同一班级的概率；
（2）从中这10名学生中，指定甲、乙、丙三人为代表，已知他们每人选择一种图书，其中选择A，B两种图书学习的概率分别是$\frac{1}{3}$，$\frac{2}{3}$，且他们选择A，B任一种图书都是相互独立的，设这三名学生中选择B的人数为ξ，求ξ的分布列和数学期望．
| 班级 | 一 | 二 | 三 | 四 |
| 人数 | 1 | 2 | 3 | 4 |
（2）从中这10名学生中，指定甲、乙、丙三人为代表，已知他们每人选择一种图书，其中选择A，B两种图书学习的概率分别是$\frac{1}{3}$，$\frac{2}{3}$，且他们选择A，B任一种图书都是相互独立的，设这三名学生中选择B的人数为ξ，求ξ的分布列和数学期望．
16．
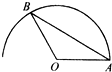如图所示，OA=1，在以O为圆心，OA为半径的半圆弧长任取一点B，则使△AOB的面积大于等于$\frac{1}{4}$的概率为（ ）
如图所示，OA=1，在以O为圆心，OA为半径的半圆弧长任取一点B，则使△AOB的面积大于等于$\frac{1}{4}$的概率为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |