题目内容
17.研究函数y=$\sqrt{x}$与函数y=$\frac{1}{4}$x2-2在[0,+∞)上的变化情况.分析 可以画出y=$\sqrt{x}$与函数y=$\frac{1}{4}{x}^{2}-2$上的图象,根据图象会发现这两个图象有一个交点,并且会发现x=4时,这两函数的函数值相等,从而根据图象便可描述这两个函数的大小的变化过程.
解答 解:可以画出函数$y=\sqrt{x}$及y=$\frac{1}{4}{x}^{2}-2$在[0,+∞)上的图象: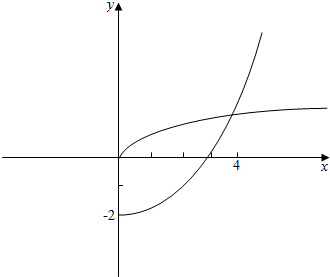
由图象可看出:
0≤x<4时,$\sqrt{x}>\frac{1}{4}{x}^{2}-2$;
x=4时,$\sqrt{x}=\frac{1}{4}{x}^{2}-2$;
x>4时,$\sqrt{x}<\frac{1}{4}{x}^{2}-2$.
点评 考查对函数$y=\sqrt{x}$和二次函数图象的掌握,借助于图象判断两个函数的大小关系变化过程的方法.

练习册系列答案
相关题目
2.y=$\frac{{\sqrt{3}}}{2}$cosα+$\frac{1}{2}$sinα的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | 2 |
9.过点A(1,2)且与点P(3,2)距离最大的直线方程是( )
| A. | x+2y+1=0 | B. | 2x-y-1=0 | C. | y=1 | D. | x=1 |