题目内容
设数列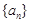 的前n项和为
的前n项和为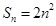 ,
, 为等比数列,且
为等比数列,且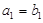 ,
,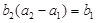
(1)求数列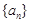 和
和 的通项公式;
的通项公式;
(2)设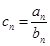 ,求数列
,求数列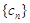 的前n项和
的前n项和 .
.
(1) ,
,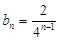 (n∈N※)
(n∈N※)
(2)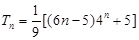 (n∈N※)
(n∈N※)
解析试题分析:(1)根据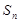 和
和 的关系,先求出
的关系,先求出 ,
,
当n≥2时, 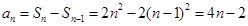
又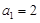 适合上式, 即
适合上式, 即 .
.
根据 为等比数列,且
为等比数列,且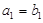 ,
,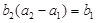 ,∴
,∴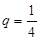
∴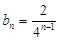 (n∈N※)
(n∈N※)
(2)由(1)得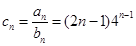 ,显然这个需要用到错位相减求和法
,显然这个需要用到错位相减求和法
∴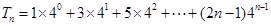
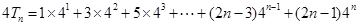
两式相减得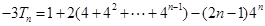 :
:
由此得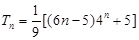 (n∈N※)
(n∈N※)
试题解析:(1)∵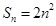
∴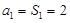 ;
;
当n≥2时, 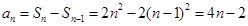
又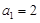 适合上式,
适合上式,
所以数列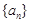 通项公式为
通项公式为 .
.
设数列 的公比为q,则由已知得
的公比为q,则由已知得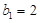 ,
,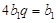
∴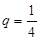
∴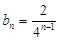 (n∈N※)
(n∈N※)
(2)由(1)得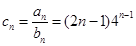
∴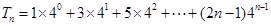
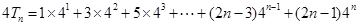
两式相减得 :
:
由此得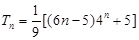 (n∈N※)
(n∈N※)
考点:等差,等比的综合题.

练习册系列答案
相关题目
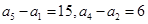 ,则
,则 _______________.
_______________.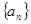 各项均为正数,前
各项均为正数,前 项和为
项和为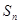 ,若
,若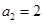 ,
,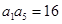 .则公比q= ,
.则公比q= ,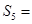 .
.  中,
中, ,
, ,
, ,
, 分别为△ABC的三个内角A,B,C的对边,且
分别为△ABC的三个内角A,B,C的对边,且 .
.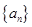 的公比
的公比 ;
; ,且
,且 ,求数列
,求数列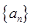 的首项
的首项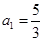 ,
,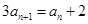 ,
, ,
, 为等比数列;
为等比数列; ,求最大的正整数
,求最大的正整数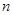 .
.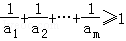 ?若存在,求m的最小值;若不存在,说明理由.
?若存在,求m的最小值;若不存在,说明理由.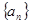 中,
中,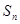 是前
是前 项和,且
项和,且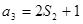 ,
,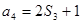 ,则公比
,则公比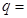 .
.