题目内容
6.已知数列{an}满足a1+2a2+3a3+…+nan=n(n∈N*).(1)求数列{an}的通项公式an;
(2)令bn=anan+2(n∈N*),Tn=b1+b2+…+bn,求证:Tn<$\frac{3}{2}$.
分析 (1)将n换为n-1,相减可得an=$\frac{1}{n}$,检验n=1也成立;
(2)由$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),运用裂项相消求和和不等式的性质,即可得证.
解答 解:(1)∵a1+2a2+3a3+…+nan=n,
a1+2a2+3a3+…+(n-1)an-1=n-1,(n>1)
两式相减得${a_n}=\frac{1}{n}(n≥2)$,
又a1=1,∴${a_n}=\frac{1}{n}(n∈{N^*})$.
(2)证明:bn=anan+2(n∈N*),Tn=b1+b2+…+bn=$\frac{1}{1•3}$+$\frac{1}{2•4}$+…+$\frac{1}{n(n+2)}$,
则${T_n}=\frac{1}{2}(1-\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{n-2}-\frac{1}{n}+\frac{1}{n-1}-\frac{1}{n+1}+\frac{1}{n}-\frac{1}{n+2})$
=$\frac{1}{2}$($\frac{3}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)<$\frac{3}{4}$<$\frac{3}{2}$.
点评 本题考查数列的通项的求法,注意运用下标变换法,同时考查数列的求和方法:裂项相消求和和不等式的性质,属于中档题.

练习册系列答案
相关题目
11.下列函数中,既是奇函数又在[0,1]上单调递增的是( )
| A. | y=|x|•x3 | B. | y=xlnx | C. | y=x•cosx | D. | $y=-x-\frac{1}{x}$ |
16.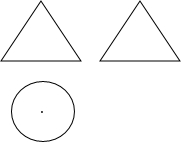 图中的三视图表示的几何体为( )
图中的三视图表示的几何体为( )
 图中的三视图表示的几何体为( )
图中的三视图表示的几何体为( )| A. | 圆柱 | B. | 圆锥 | C. | 圆台 | D. | 三棱柱 |