Question

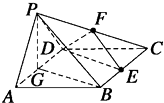
【题目】如图所示，在四棱锥P﹣ABCD中，底面ABCD是∠DAB=60°且边长为a的菱形，侧面PAD为正三角形，其所在平面垂直于底面ABCD，若G为AD边的中点，
（1）求证：BG⊥平面PAD；
（2）求证：AD⊥PB；
（3）若E为BC边的中点，能否在棱PC上找到一点F，使平面DEF⊥平面ABCD，并证明你的结论．

Answer 1

【答案】
（1）证明：在底面菱形ABCD中，∠DAB=60°，G为AD边的中点，所以BG⊥AD，

又平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，

所以BG⊥平面PAD

（2）证明：连接PG，因为△PAD为正三角形，

G为AD边的中点，

得PG⊥AD，由（1）知BG⊥AD，

PG平面PGB，BG平面PGB，PG∩BG=G，

所以AD⊥平面PGB，因为PB平面PGB．

所以AD⊥PB

（3）解：当F为PC边的中点时，满足平面DEF⊥平面ABCD，证明如下：

取PC 的中点F，连接DE、EF、DF，

在△PBC中，FE∥PB，在菱形ABCD中，GB∥DE，

EF∩DE=E，所以平面DEF∥平面PGB，因为BG⊥平面PAD，所以BG⊥PG，又因为PG⊥AD，AD∩BG=G，

∴PG⊥平面ABCD，而PG平面PGB，

所以平面PGB⊥平面ABCD，

所以平面DEF⊥平面ABCD．

【解析】（1）证明BG⊥AD，通过平面与平面垂直的性质，即可证明BG⊥平面PAD．（2）连接PG，证明PG⊥AD，通过BG⊥AD，证明AD⊥平面PGB，然后证明AD⊥PB．（3）当F为PC边的中点时，满足平面DEF⊥平面ABCD，证明如下：取PC 的中点F，连接DE、EF、DF，

通过证明BG⊥PG，PG⊥AD，AD∩BG=G，PG⊥平面ABCD，即可证明平面DEF⊥平面ABCD．

【考点精析】本题主要考查了直线与平面垂直的判定和平面与平面垂直的判定的相关知识点，需要掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想；一个平面过另一个平面的垂线，则这两个平面垂直才能正确解答此题．