题目内容
【题目】已知椭圆C的中心在坐标原点O,其右焦点为F(1,0),以坐标原点O为圆心,椭圆短半轴长为半径的圆与直线x﹣y![]() 0的相切.
0的相切.
(1)求椭圆C的方程;
(2)经过点F的直线l1,l2分别交椭圆C于A、B及C、D四点,且l1⊥l2,探究:是否存在常数λ,使![]() 恒成立.
恒成立.
【答案】(1)![]() ;(2)存在常数
;(2)存在常数![]() 使得
使得![]() 恒成立,详见解析.
恒成立,详见解析.
【解析】
(1)根据点到直线的距离可以求出短半轴长b,因为焦点已知,所以c=1,根据a2=b2+c2可以求得a2,从而确定椭圆的方程;
(2)分两类,①l1,l2中一条斜率不存在,②l1,l2的斜率存在且不为0,分别来探索常数λ的值,其中在情形②中,需要设l1:x=ty+1(t≠0),![]() ,然后联立直线方程和椭圆的方程,消去x得到关于y的方程,再利用弦长公式分别求出|AB|和|CD|,并代入到
,然后联立直线方程和椭圆的方程,消去x得到关于y的方程,再利用弦长公式分别求出|AB|和|CD|,并代入到![]() 化简即可得解.
化简即可得解.
(1)设所求的椭圆方程为![]() ,
,
点O到直线x﹣y![]() 0的距离为
0的距离为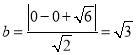 ,
,
又c=1,∴a2=b2+c2=4,
故所求的椭圆C的方程为![]() .
.
(2)假设存在常数λ,使![]() 恒成立,则
恒成立,则![]() ,
,
①当l1,l2中一条斜率不存在时,可知|AB|,|CD|其中一个长为2a=4,另一个为![]() ,
,
此时![]() ,
,
②当l1,l2的斜率存在且不为0时,不妨设l1:x=ty+1(t≠0),![]() ,
,
A(ty1+1,y1),B(ty2+1),
联立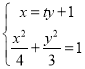 得(3t2+4)y2+6ty﹣9=0,
得(3t2+4)y2+6ty﹣9=0,
∴![]() ,
,![]() ,
,![]() =36t2﹣4(3t2+4)(﹣9)=144(t2+1)>0,
=36t2﹣4(3t2+4)(﹣9)=144(t2+1)>0,
∴![]() ,
,
用![]() 代替上式中的t可得,
代替上式中的t可得,![]() ,
,
∴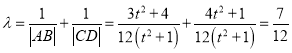 ,
,
综上所述,存在常数![]() 使得
使得![]() 恒成立.
恒成立.

 智慧小复习系列答案
智慧小复习系列答案【题目】某中学高三(3)班全班50人参加了高考前的数学模拟测试,每名学生要在规定的2个小时内做一套高三模拟卷,现抽取10位学生的成绩,分为甲,乙两组,其分数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | |
甲组 | 64 | 72 | 86 | 98 | 120 |
乙组 | 60 | 76 | 90 | 92 | 122 |
(Ⅰ)分别求出甲,乙两组学生考试所得分数的平均数及方差,并由此分析两组学生的成绩水平;
(Ⅱ)试估计全班有多少人及格(90分及以上为及格);
(Ⅲ)从该班级甲,乙两组中各随机抽取1名学生,对其考试成绩进行抽查,求两人考试分数之和大于等于180的概率.
【题目】福利彩票“双色球”中红色球由编号为![]() 的
的![]() 个球组成.某彩民利用下面的随机数表选取
个球组成.某彩民利用下面的随机数表选取![]() 组数作为
组数作为![]() 个红色球的编号,选取方法是从随机数表(如下)第
个红色球的编号,选取方法是从随机数表(如下)第![]() 行的第
行的第![]() 列数字开始从左向右依次选取两个数字,则选出来的第
列数字开始从左向右依次选取两个数字,则选出来的第![]() 个红色球的编号为( )
个红色球的编号为( )
49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 17 34 91 64 |
57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()