题目内容
(本小题满分12分)
已知直线l上有一列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,其 中n∈N*,x1=1,x2=2,点Pn+2分有向线段
中n∈N*,x1=1,x2=2,点Pn+2分有向线段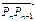 所成的比为λ(λ≠-1).
所成的比为λ(λ≠-1).
(1)写出xn+2与xn+1,xn之间的关系式;
(2)设an=xn+1-xn,求数列{an}的通项公式.
已知直线l上有一列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,其
 中n∈N*,x1=1,x2=2,点Pn+2分有向线段
中n∈N*,x1=1,x2=2,点Pn+2分有向线段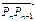 所成的比为λ(λ≠-1).
所成的比为λ(λ≠-1).(1)写出xn+2与xn+1,xn之间的关系式;
(2)设an=xn+1-xn,求数列{an}的通项公式.
解:(1)由定比分点坐标公式得xn+2= .…………………6分
.…………………6分
(2)a1=x2-x1=1, an+1=xn+2-xn+1= -x
-x n+1=-
n+1=- (xn+1-xn)=-
(xn+1-xn)=- an,
an,
∴ =-
=- ,即{an}是以a1=1为首项,-
,即{an}是以a1=1为首项,- 为公比的等比数列.
为公比的等比数列.
∴an=(- )n-1
)n-1 . …………………12分
. …………………12分
 .…………………6分
.…………………6分(2)a1=x2-x1=1, an+1=xn+2-xn+1=
 -x
-x n+1=-
n+1=- (xn+1-xn)=-
(xn+1-xn)=- an,
an,∴
 =-
=- ,即{an}是以a1=1为首项,-
,即{an}是以a1=1为首项,- 为公比的等比数列.
为公比的等比数列.∴an=(-
 )n-1
)n-1 . …………………12分
. …………………12分略

练习册系列答案
相关题目
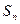 是数列
是数列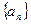 的前
的前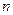 项和,且
项和,且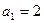 ,
,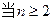 时有
时有 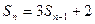 .
.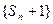 是等比数列;
是等比数列; ,公比|q|≠1,若am= a1·a2· a3· a4· a5,则m=( )
,公比|q|≠1,若am= a1·a2· a3· a4· a5,则m=( )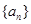 为等比数列,且满足
为等比数列,且满足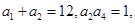 则
则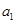 =( )
=( )
 或16
或16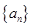 是任意等比数列,它的前
是任意等比数列,它的前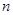 项和,前
项和,前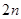 项和与前
项和与前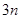 项和分别为
项和分别为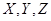 ,
,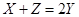



 的公比
的公比 ,前
,前 项和为
项和为 ,则
,则 _____________
_____________ 中,
中, 则公比
则公比
 的前
的前 项和为
项和为 若
若 是公差为
是公差为 的等差数列,则
的等差数列,则 为等差数列时
为等差数列时 ▲
▲  .
.