题目内容
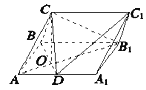
【题目】在三棱柱ABC﹣A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点.
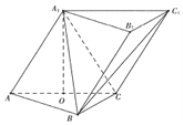
(Ⅰ)证明:A1O⊥平面ABC;
(Ⅱ)求三棱锥C1﹣ABC的体积.
【答案】(Ⅰ)见解析; (Ⅱ)1.
【解析】试题分析:(Ⅰ)由面面垂直的判定定理证明;(Ⅱ)因为![]() 平面
平面![]() ,所以点
,所以点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,而由(Ⅰ)有:A1O⊥平面ABC,所以
的距离,而由(Ⅰ)有:A1O⊥平面ABC,所以![]() 为点
为点![]() 到平面
到平面![]() 的距离,再用椎体体积公式求出体积.
的距离,再用椎体体积公式求出体积.
试题解析:证明:(Ⅰ)∵AA1=A1C,且O为AC的中点,
∴A1O⊥AC,
又∵平面AA1C1C⊥平面ABC,
平面AA1C1C∩平面ABC=AC
且A1O平面AA1C1C,
∴A1O⊥平面ABC
(Ⅱ)∵A1C1∥AC,A1C1平面ABC,AC平面ABC,
∴A1C1∥平面ABC,
即C1到平面ABC的距离等于A1到平面ABC的距离
由(Ⅰ)知A1O⊥平面ABC且![]() ,
,
∴三棱锥C1﹣ABC的体积:
![]()

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
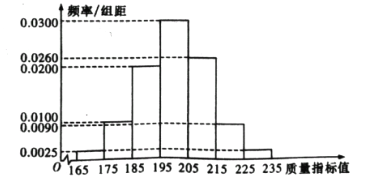
(1)根据以上抽样调查数据 ,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(2)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?