题目内容
(2013•临沂一模)已知函数f(x)=cos
-
sin
.
(I)若x∈[-2π,2π],求函数f(x)的单调减区间;
(Ⅱ)在△ABC中,a,b,c分别为角A,B,C的对边,若f(2A-
π)=
,sinB=
cosC,a=
,求△ABC的面积.
| x |
| 2 |
| 3 |
| x |
| 2 |
(I)若x∈[-2π,2π],求函数f(x)的单调减区间;
(Ⅱ)在△ABC中,a,b,c分别为角A,B,C的对边,若f(2A-
| 2 |
| 3 |
| 4 |
| 3 |
| 5 |
| 2 |
分析:(I)先利用两角和的余弦公式化为f(x)=2cos(
+
),再利用余弦函数的单调性即可得出;
(II)由f(2A-
)=
利用(I)的结论可得cosA=
,利用平方关系可得sinA,利用
cosC=sinB=sin(A+C),及平方关系可得sinC与cosC.即可得到sinB.再利用正弦定理及三角形的面积公式可得S△=
即可得出.
| x |
| 2 |
| π |
| 3 |
(II)由f(2A-
| 2π |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 5 |
| a2 |
| 2 |
| sinBsinC |
| sinA |
解答:解:(I)函数f(x)=cos
-
sin
=2(
cos
-
sin
)=2cos(
+
),
由2kπ≤
+
≤2kπ+π,解得4kπ-
≤x≤4kπ+
,k∈Z.
∵x∈[-2π,2π],令k=0,得-
≤x≤
,
∴函数f(x)的单调减区间为[-
,
];
(II)由(I)可得:f(2A-
)=2cos(A-
+
)=
,∴cosA=
,
∵A∈(0,π),∴sinA=
=
,
又∵
cosC=sinB=sin(A+C),∴
cosC=
cosC+
sinC,
化为
cosC=sinC,∴tanC=
.
∵C∈(0,π),∴sinC=
,cosC=
,∴sinB=
cosC=
.
由正弦定理
=
,∴b=
.
∴S△=
absinC=
×
=
×
=
.
| x |
| 2 |
| 3 |
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| ||
| 2 |
| x |
| 2 |
| x |
| 2 |
| π |
| 3 |
由2kπ≤
| x |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| 4π |
| 3 |
∵x∈[-2π,2π],令k=0,得-
| 2π |
| 3 |
| 4π |
| 3 |
∴函数f(x)的单调减区间为[-
| 2π |
| 3 |
| 4π |
| 3 |
(II)由(I)可得:f(2A-
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
∵A∈(0,π),∴sinA=
| 1-cos2A |
| ||
| 3 |
又∵
| 5 |
| 5 |
| ||
| 3 |
| 2 |
| 3 |
化为
| 5 |
| 5 |
∵C∈(0,π),∴sinC=
| ||
|
| 1 | ||
|
| 5 |
| ||
|
由正弦定理
| a |
| sinA |
| b |
| sinB |
| asinB |
| sinA |
∴S△=
| 1 |
| 2 |
| a2 |
| 2 |
| sinBsinC |
| sinA |
(
| ||
| 2 |
| ||||||||||||
|
| ||
| 2 |
点评:本题综合考查了三角函数的单调性、平方关系、两角和的正弦余弦公式、正弦定理、三角形的面积公式等基础知识与方法,需要较强的推理能力和计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
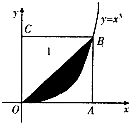 (2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
(2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )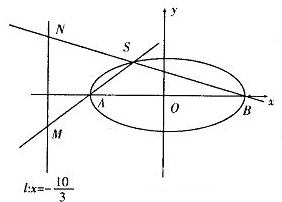 (2013•临沂一模)如图,已知椭圆C:
(2013•临沂一模)如图,已知椭圆C: