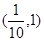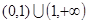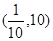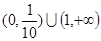题目内容
已知a>0且a≠1,若函数f (x)= loga(ax2 –x)在[3,4]是增函数,则a的取值范围是( )
| A.(1,+∞) | B.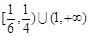 | C.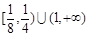 | D.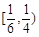 |
A
解:当a>1时,由于函数t=ax2-x在[3,4]是增函数,且函数t大于0,
故函数f (x)= loga(ax2 –x)在[3,4]是增函数,满足条件.
当 1>a>0时,由题意可得 函数t=ax2-x在[3,4]应是减函数,且函数t大于0,
故1 a ≥4,且 16a-4>0. 即 a≤1 /4 ,且 a>1/ 4 ,∴a∈∅.
综上,只有当a>1时,才能满足条件,故选 A
故函数f (x)= loga(ax2 –x)在[3,4]是增函数,满足条件.
当 1>a>0时,由题意可得 函数t=ax2-x在[3,4]应是减函数,且函数t大于0,
故1 a ≥4,且 16a-4>0. 即 a≤1 /4 ,且 a>1/ 4 ,∴a∈∅.
综上,只有当a>1时,才能满足条件,故选 A

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
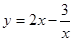 在区间
在区间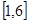 上的最小值为________,最大值为________
上的最小值为________,最大值为________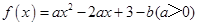 在
在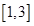 有最大值5和最小值2,求a、b的值。
有最大值5和最小值2,求a、b的值。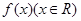 满足:
满足: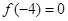 ,且在区间
,且在区间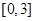 与
与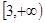 上分别递减和递增,则不等式
上分别递减和递增,则不等式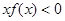 的解集为_____.
的解集为_____.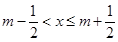 (其中
(其中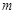 为整数),则
为整数),则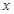 最近的整数,记作
最近的整数,记作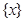 ,
,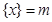 . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数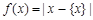 的四个命题:
的四个命题: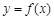 的定义域是R,值域是[0,
的定义域是R,值域是[0,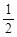 ];
];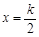 (k∈Z)对称;
(k∈Z)对称;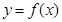 在
在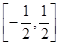 上是增函数;
上是增函数; 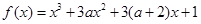 有极大值和极小值,则
有极大值和极小值,则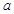 的取值范围是( )
的取值范围是( )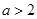 或
或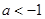
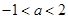
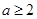 或
或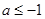
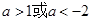
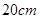 的铁丝剪成两段,并分别折成正方形,则这两个正方形的面积的和的最小值为( )
的铁丝剪成两段,并分别折成正方形,则这两个正方形的面积的和的最小值为( )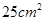
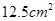
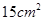

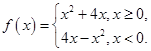 若
若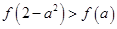 ,则实数
,则实数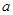 的取值范围是( )
的取值范围是( )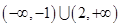
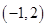
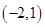
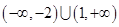
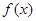 为偶函数,它在
为偶函数,它在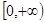 上减函数,若
上减函数,若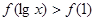 ,则x的取值范围是( )
,则x的取值范围是( )