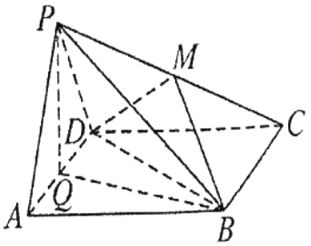
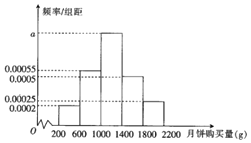
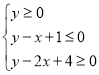题目内容
【题目】以直角坐标系xOy的坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程是![]() ,曲线C2的参数方程是
,曲线C2的参数方程是![]() (θ为参数).
(θ为参数).
(1)写出曲线C1,C2的普通方程;
(2)设曲线C1与y轴相交于A,B两点,点P为曲线C2上任一点,求|PA|2+|PB|2的取值范围.
【答案】(1) 曲线C1的普通方程为![]() .曲线C2的普通方程为(x-2)2+(y-2)2=4.(2) [32-16
.曲线C2的普通方程为(x-2)2+(y-2)2=4.(2) [32-16![]() ,32+16
,32+16![]() ].
].
【解析】
(1)由题得![]() ,再把极坐标化成直角坐标,得到C1的普通方程;消参得到C2的普通方程;(2)设P(2+2cosθ,2+2sinθ),求出|PA|2+|PB|2=
,再把极坐标化成直角坐标,得到C1的普通方程;消参得到C2的普通方程;(2)设P(2+2cosθ,2+2sinθ),求出|PA|2+|PB|2=![]()
![]() ,再求其取值范围.
,再求其取值范围.
(1)由![]() ,得
,得![]() .
.
∴![]() ,4ρ2cos2θ+9ρ2sin2θ=36.∴4x2+9y2=36,
,4ρ2cos2θ+9ρ2sin2θ=36.∴4x2+9y2=36,
即曲线C1的普通方程为![]() .
.
曲线C2的普通方程为(x-2)2+(y-2)2=4.
(2)由(1)知,点A,B的坐标分别为(0,2),(0,-2),设P(2+2cosθ,2+2sinθ),
则|PA|2+|PB|2=(2+2cosθ)2+(2sinθ)2+(2+2cosθ)2+(4+2sinθ)2=32+16sinθ+16cosθ![]() .
.
∴|PA|2+|PB|2∈[32-16![]() ,32+16
,32+16![]() ],
],
即|PA|2+|PB|2的取值范围是[32-16![]() ,32+16
,32+16![]() ].
].

练习册系列答案
相关题目