题目内容
已知椭圆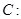
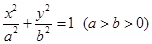 的左、右焦点分别为
的左、右焦点分别为 、
、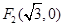 ,椭圆上的点
,椭圆上的点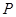 满足
满足 ,且
,且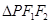 的面积
的面积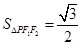 .
.
(Ⅰ)求椭圆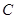 的方程;
的方程;
(Ⅱ)是否存在直线 ,使
,使 与椭圆
与椭圆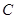 交于不同的两点
交于不同的两点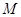 、
、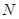 ,且线段
,且线段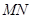 恰被直线
恰被直线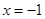 平分?若存在,求出
平分?若存在,求出 的斜率取值范围;若不存在,请说明理由.
的斜率取值范围;若不存在,请说明理由.
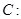
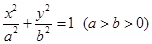 的左、右焦点分别为
的左、右焦点分别为 、
、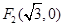 ,椭圆上的点
,椭圆上的点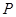 满足
满足 ,且
,且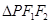 的面积
的面积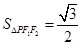 .
.(Ⅰ)求椭圆
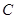 的方程;
的方程;(Ⅱ)是否存在直线
 ,使
,使 与椭圆
与椭圆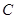 交于不同的两点
交于不同的两点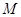 、
、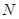 ,且线段
,且线段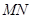 恰被直线
恰被直线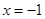 平分?若存在,求出
平分?若存在,求出 的斜率取值范围;若不存在,请说明理由.
的斜率取值范围;若不存在,请说明理由.(I)椭圆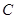 的方程为
的方程为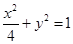 .(Ⅱ)存在满足题设条件的直线
.(Ⅱ)存在满足题设条件的直线 ,且
,且 的斜率取值范围是
的斜率取值范围是
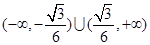 .
.
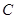 的方程为
的方程为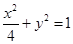 .(Ⅱ)存在满足题设条件的直线
.(Ⅱ)存在满足题设条件的直线 ,且
,且 的斜率取值范围是
的斜率取值范围是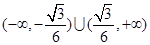 .
.试题分析:(Ⅰ)由题意知:
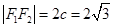 .
. ,且
,且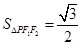 ,由此可求得
,由此可求得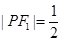 ,
,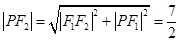 ,二者相加即得
,二者相加即得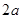 ,从而得椭圆的方程. (Ⅱ)假设这样的直线
,从而得椭圆的方程. (Ⅱ)假设这样的直线 存在,且直线
存在,且直线 的方程为
的方程为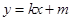 ,设
,设 与椭圆
与椭圆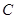 的两交点为
的两交点为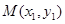 、
、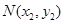 ,若线段
,若线段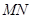 恰被直线
恰被直线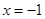 平分,则
平分,则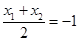 .这显然用韦达定理.由
.这显然用韦达定理.由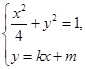 得
得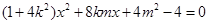 .
. 由
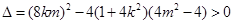 得
得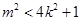 .再用韦达定理得
.再用韦达定理得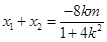 ,代入
,代入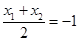 得
得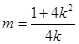 ,再将此式代入
,再将此式代入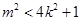 得一只含
得一只含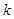 的不等式,解此不等式即得
的不等式,解此不等式即得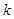 的取值范围.
的取值范围. 试题解析:(Ⅰ)由题意知:
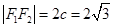 , (1分)
, (1分)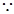 椭圆上的点
椭圆上的点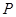 满足
满足 ,且
,且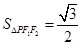 ,
,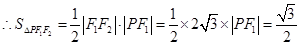 .
.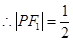 ,
,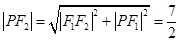 .
.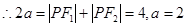 . (2分)
. (2分)又
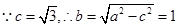 . (3分)
. (3分)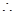 椭圆
椭圆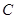 的方程为
的方程为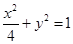 . (4分)
. (4分)(Ⅱ)假设这样的直线
 存在.
存在.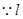 与直线
与直线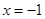 相交,
相交, 直线
直线 的斜率存在.
的斜率存在.设
 的方程为
的方程为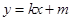 , (5分)
, (5分)由
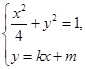 得
得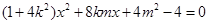 .(*) (6分)
.(*) (6分)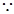 直线
直线 与椭圆
与椭圆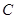 有两个交点,
有两个交点,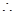 (*)的判别式
(*)的判别式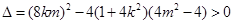 ,即
,即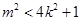 .① (7分)
.① (7分)设
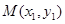 、
、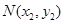 ,则
,则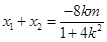 . (8分)
. (8分)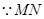 被直线
被直线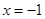 平分,可知
平分,可知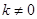 ,
,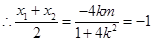 ,
,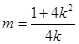 . ② (9分)
. ② (9分)把②代入①,得
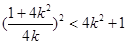 ,即
,即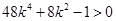 . (10分)
. (10分)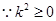 ,
,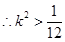 . (11分)
. (11分)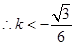 或
或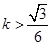 .即存在满足题设条件的直线
.即存在满足题设条件的直线 ,且
,且 的斜率取值范围是
的斜率取值范围是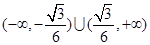 . (12分)
. (12分)
练习册系列答案
相关题目
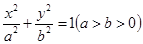 的左、右焦点和短轴的一个端点构成边长为4的正三角形.
的左、右焦点和短轴的一个端点构成边长为4的正三角形.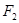 的直线
的直线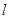 与椭圆C相交于A、B两点,若
与椭圆C相交于A、B两点,若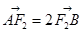 ,求直线
,求直线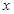 轴的抛物线经过点
轴的抛物线经过点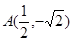 .
.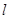 过定点
过定点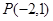 ,斜率为
,斜率为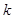 ,当
,当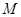 :
: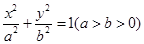 经过点
经过点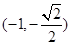 ,
,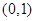 .
.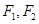 ,过点
,过点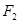 的直线交椭圆
的直线交椭圆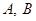 两点,求
两点,求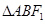 面积的最大值.
面积的最大值.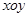 中,已知
中,已知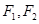 分别是椭圆
分别是椭圆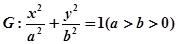 的左、右焦点,椭圆
的左、右焦点,椭圆 与抛物线
与抛物线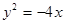 有一个公共的焦点,且过点
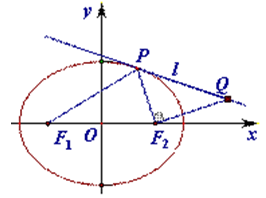
有一个公共的焦点,且过点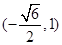 .
.
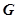 的方程;
的方程;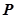 是椭圆
是椭圆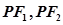 ,过
,过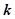 的直线
的直线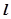 ,使得
,使得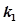 ,
,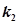 ,试证明
,试证明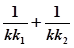 为定值,并求出这个定值;
为定值,并求出这个定值;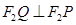 ,设
,设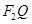 交
交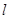 于点
于点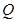 ,
,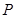 在椭圆上移动时,点
在椭圆上移动时,点 在抛物线
在抛物线 :
: 上.
上. 的三个顶点都在抛物线
的三个顶点都在抛物线 ,
, ,
, 所在直线的斜率分别为
所在直线的斜率分别为 ,
, ,
, ,求
,求 的值;
的值; 的四个顶点都在抛物线
的四个顶点都在抛物线 ,
, 所在直线的斜率分别为
所在直线的斜率分别为 ,求
,求 的值.
的值.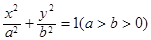 的左、右焦点分别为
的左、右焦点分别为 ,且
,且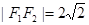 ,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.
,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.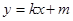 相交于不同的两点M、N,又点
相交于不同的两点M、N,又点 ,当
,当 时,求实数m的取值范围,
时,求实数m的取值范围, 及定点
及定点 ,点
,点 是圆
是圆 上的动点,点
上的动点,点 在
在 上,且满足
上,且满足 ,
, 。
。 关于直线
关于直线 的对称点在曲线
的对称点在曲线 的取值范围。
的取值范围。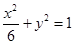 共焦点,且渐近线为
共焦点,且渐近线为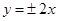 的双曲线方程是( )
的双曲线方程是( )