题目内容
已知椭圆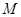 :
: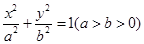 经过点
经过点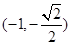 ,
,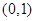 .
.
(Ⅰ)求椭圆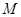 的方程;
的方程;
(Ⅱ)设椭圆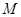 的左、右焦点分别为
的左、右焦点分别为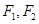 ,过点
,过点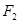 的直线交椭圆
的直线交椭圆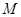 于
于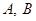 两点,求
两点,求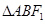 面积的最大值.
面积的最大值.
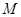 :
: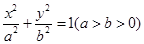 经过点
经过点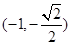 ,
,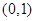 .
.(Ⅰ)求椭圆
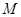 的方程;
的方程;(Ⅱ)设椭圆
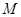 的左、右焦点分别为
的左、右焦点分别为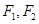 ,过点
,过点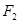 的直线交椭圆
的直线交椭圆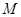 于
于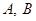 两点,求
两点,求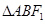 面积的最大值.
面积的最大值.(Ⅰ)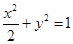 ;(Ⅱ)
;(Ⅱ)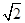
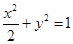 ;(Ⅱ)
;(Ⅱ)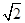
试题分析:(Ⅰ)将两点坐标代入椭圆方程组成方程组,即可求
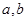 的值。(Ⅱ)由椭圆方程可知
的值。(Ⅱ)由椭圆方程可知 。可分直线斜率存在和不存在两种情况讨论,为了省去讨论也可直接设直线
。可分直线斜率存在和不存在两种情况讨论,为了省去讨论也可直接设直线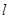 方程为
方程为 。与椭圆联立方程,消去
。与椭圆联立方程,消去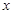 整理可得关于
整理可得关于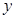 的一元二次方程,因为有两个交点即方程有两根,所以判别式应大于0。然后用韦达定理得根与系数的关系。求
的一元二次方程,因为有两个交点即方程有两根,所以判别式应大于0。然后用韦达定理得根与系数的关系。求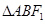 面积时可先求截得的弦长,再求点
面积时可先求截得的弦长,再求点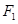 到直线的距离,从而可求面积(此种方法计算量过大)。另一方法求
到直线的距离,从而可求面积(此种方法计算量过大)。另一方法求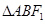 面积:可用转化思想将
面积:可用转化思想将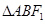 分解成两个小三角形,即
分解成两个小三角形,即 。因为
。因为 ,可转化为二次函数求最值问题。
,可转化为二次函数求最值问题。试题解析:解:(Ⅰ)由题意
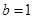 ,椭圆
,椭圆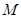 的方程为
的方程为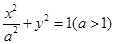 . 1分
. 1分将点
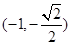 代入椭圆方程,得
代入椭圆方程,得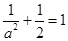 ,解得
,解得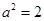 .
. 所以 椭圆
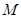 的方程为
的方程为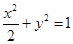 . 3分
. 3分(Ⅱ)由题意可设直线
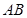 的方程为:
的方程为: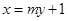 .
.由
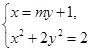 得
得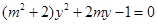 .
.显然
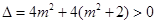 .
.设
 ,
,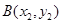 ,则
,则 7分
7分因为
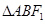 的面积
的面积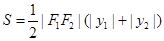 ,其中
,其中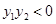 .
.所以
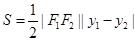 .
.又

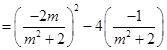
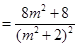 ,
,  . 9分
. 9分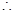
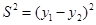
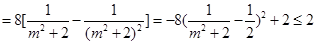 .
.当
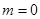 时,上式中等号成立.
时,上式中等号成立.即当
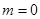 时,
时,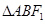 的面积取到最大值
的面积取到最大值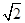 . 11分
. 11分
练习册系列答案
相关题目
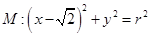
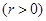 ,若椭圆
,若椭圆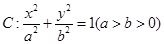 的右顶点为圆
的右顶点为圆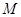 的圆心,离心率为
的圆心,离心率为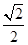 .
.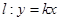 ,使得直线
,使得直线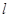 与椭圆
与椭圆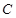 分别交于
分别交于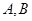 两点,与圆
两点,与圆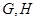 两点,点
两点,点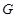 在线段
在线段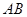 上,且
上,且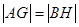 ,求圆
,求圆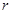 的取值范围.
的取值范围.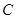 的顶在坐标原点,焦点
的顶在坐标原点,焦点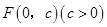 到直线
到直线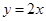 的距离是
的距离是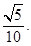
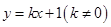 与抛物线
与抛物线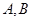 两点,设线段
两点,设线段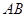 的中垂线与
的中垂线与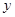 轴交于点
轴交于点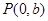 ,求
,求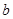 的取值范围.
的取值范围. ,点
,点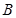 在直线
在直线 :
: 上运动,过点
上运动,过点 的垂直平分线相交于点
的垂直平分线相交于点 .
.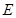 的方程;
的方程;
 作两条直线分别与轨迹
作两条直线分别与轨迹 ,
,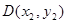 两点.试探究:当直线
两点.试探究:当直线 ,
, 的斜率存在且倾斜角互补时,直线
的斜率存在且倾斜角互补时,直线 的斜率是否为定值?若是,求出这个定值;若不是,说明理由.
的斜率是否为定值?若是,求出这个定值;若不是,说明理由.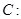
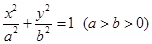 的左、右焦点分别为
的左、右焦点分别为 、
、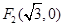 ,椭圆上的点
,椭圆上的点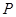 满足
满足 ,且
,且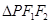 的面积
的面积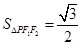 .
.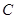 的方程;
的方程; ,使
,使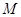 、
、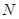 ,且线段
,且线段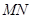 恰被直线
恰被直线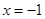 平分?若存在,求出
平分?若存在,求出 与椭圆E相交于P,Q两点,且
与椭圆E相交于P,Q两点,且 的最大值为
的最大值为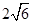 .
.
 ,过点P且平行于y轴的直线与椭圆E相交于另一点M,试问M,F,Q是否共线,若共线请证明;反之说明理由.
,过点P且平行于y轴的直线与椭圆E相交于另一点M,试问M,F,Q是否共线,若共线请证明;反之说明理由.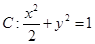 的左、右焦点分别为
的左、右焦点分别为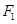 、
、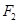 ,
,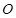 为原点.
为原点.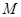 为椭圆
为椭圆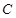 上的一点,
上的一点,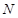 是
是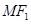 的中点,且
的中点,且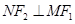 ,求点
,求点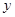 轴的距离;
轴的距离;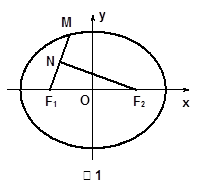
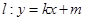 与椭圆
与椭圆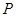 、
、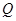 两点,若在椭圆
两点,若在椭圆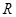 ,使四边形
,使四边形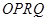 为平行四边形,求
为平行四边形,求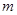 的取值范围.
的取值范围.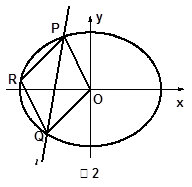
 、
、 是过抛物线
是过抛物线 焦点
焦点 的两条弦,且其焦点
的两条弦,且其焦点 ,
, ,点
,点 为
为 轴上一点,记
轴上一点,记 ,其中
,其中 为锐角.
为锐角.
 .
.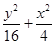 =1,椭圆C2以C1的短轴为长轴,且与C1有相同的离心率.
=1,椭圆C2以C1的短轴为长轴,且与C1有相同的离心率.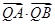 =4,求直线l的方程.
=4,求直线l的方程.