题目内容
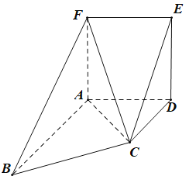
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,若
,若![]() 为
为![]() 的中点.
的中点.
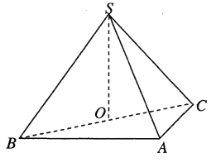
(1)证明:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 和
和![]() 所成角;
所成角;
(3)设线段![]() 上有一点
上有一点![]() ,当
,当![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() (3)
(3)![]() .
.
【解析】
(1)先证明平面![]() 平面
平面![]() ,再证明
,再证明![]() 平面
平面![]() ;(2)分别以
;(2)分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的非负半轴,建立空间直角坐标系,利用向量法求异面直线
轴的非负半轴,建立空间直角坐标系,利用向量法求异面直线![]() 和
和![]() 所成角;(3)设
所成角;(3)设![]() ,
,![]() ,利用向量法得到
,利用向量法得到![]() ,解方程即得t的值和
,解方程即得t的值和![]() 的长.
的长.
(1)∵![]() ,
,![]() ,
,
∴![]() ,
,
∵平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
如图,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的非负半轴,建立空间直角坐标系,
轴的非负半轴,建立空间直角坐标系,
∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵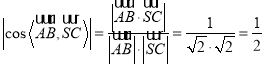 ,
,
∴异面直线![]() 和
和![]() 所成角为
所成角为![]() .
.
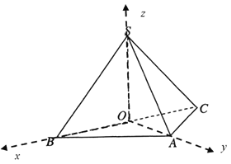
(3)设![]() 为平面
为平面![]() 的法向量,
的法向量,
∵![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
设![]() ,
,![]() ,
,
∴![]() ,
,
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
∵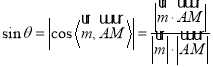 ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (舍),
(舍),![]() ,
,
∴![]() 的长为
的长为![]() .
.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|

(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.