题目内容
18.定义两个互相垂直的单位向量为“一对单位正交向量”,设平面向量a i(i=1,2,3,4)满足条件:|ai|=1(i=1,2,3,4)且ai•ai+1=0(i=1,2,3),则( )| A. | a1+a2+a3+a4=0 | |
| B. | |a1+a2+a3+a4|=2或2$\sqrt{2}$ | |
| C. | ai(i=1,2,3,4)中任意两个都是一对单位正交向量 | |
| D. | a1,a4是一对单位正交向量 |
分析 ai•ai+1=0(i=1,2,3),可得a1=a3或a1=-a3.a2=a4或a2=-a4.即可排除A,B,C.得出正确答案.
解答 解:∵ai•ai+1=0(i=1,2,3),∴a1=a3或a1=-a3.a2=a4或a2=-a4.
∴可取a1=(1,0),a2=(0,1),a3=(1,0),a4=(0,1)或(0,-1).
a1=(1,0),a2=(0,1),a3=(-1,0),a4=(0,1)或(0,-1).
取a2=(0,-1)同样可得.
即可排除A,B,C.
因此D正确.
故选:D.
点评 本题考查了向量垂直与数量积的关系、排除法,考查了推理能力与技能数列,属于中档题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
9.已知x>y>0,a=log2(x3+y3),b=log2(x2y+xy2),c=1+$\frac{3}{2}$log2xy,则( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | c>b>a |
13.执行如图所示的程序框图,则输出的S的值为( )


| A. | 1023 | B. | 1024 | C. | 2047 | D. | 2048 |
3.已知函数f(x)=$\frac{2x+3}{3x}$,数列{an}满足a1=1,an+1=f($\frac{1}{{a}_{n}}$),n∈N*.数列{an}的通项公式;( )
| A. | an=$\frac{2}{3}$n+$\frac{1}{3}$ | B. | an=$\frac{2}{3}$n-$\frac{1}{3}$ | C. | an=$\frac{1}{3}$n+$\frac{1}{3}$ | D. | an=$\frac{2}{3}$n+$\frac{1}{4}$ |
10.已知函数f(x)=-x2+2ax+1-a在区间[0,1]上的最大值为2,则a的值为( )
| A. | 2 | B. | -1或-3 | C. | 2或-3 | D. | -1或2 |
6.若a为实数,且2+ai=(1+i)(3+i),则a=( )
| A. | -4 | B. | -3 | C. | 3 | D. | 4 |
7.若非零实数x,y,z满足2x=3y=6z,则$\frac{x+y}{z}$∈( )
| A. | (5,6) | B. | (4,5) | C. | (3,4) | D. | (2,3) |
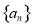 的前
的前 项和为
项和为 ,
, .
. 和
和 ;
; 的前
的前 项和为
项和为 ,证明:
,证明: .
.