题目内容

设F₁，F₂是双曲线 $数学公式$ 的两个焦点，点P在双曲线上，且∠F₁PF₂=90°，求△F₁PF₂的面积．

解：双曲线 $\text{[math]}$ 的a=3，c=5，
不妨设PF₁＞PF₂，则PF₁-PF₂=2a=6F₁F₂²=PF₁²+PF₂²，而F₁F₂=2c=10
得PF₁²+PF₂²=（PF₁-PF₂）²+2PF₁•PF₂=100
∴PF₁•PF₂=32
∴ $\text{[math]}$
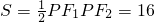
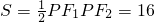
△F₁PF₂的面积16．
分析：根据根据双曲线性质可知PF₁-PF₂的值，再根据∠F₁PF₂=90°，求得PF₁²+PF₂²的值，进而根据余弦定理求得PF₁•PF₂，进而可求得△F₁PF₂的面积．
点评：本题主要考查了双曲线的简单性质．要灵活运用双曲线的定义及焦距、实轴、虚轴等之间的关系．

练习册系列答案

出彩同步大试卷系列答案

黄冈状元成才路状元导学案系列答案

全优天天练系列答案

学习高手课时作业系列答案

鲁西图书课时训练系列答案

优学3部曲初中生随堂检测系列答案

非常听力系列答案

优效作业本系列答案

天利38套对接高考小题轻松练系列答案

抢先起跑提优大试卷系列答案

相关题目

设F₁，F₂是双曲线

=1（a＞0，b＞0）的两个焦点，点P在双曲线上，若

），则双曲线的离心率为（　　）

（2010•宝山区模拟）双曲线C：

=1上一点(2，

)到左，右两焦点距离的差为2．
（1）求双曲线的方程；
（2）设F₁，F₂是双曲线的左右焦点，P是双曲线上的点，若|PF₁|+|PF₂|=6，求△PF₁F₂的面积；
（3）过（-2，0）作直线l交双曲线C于A，B两点，若

，是否存在这样的直线l，使OAPB为矩形？若存在，求出l的方程，若不存在，说明理由．

设F₁、F₂是双曲线x2-

=1的两个焦点，是双曲线上的一点，且3|PF₁|=4|PF₂|，则△PF₁F₂的面积等于

（2013•许昌三模）设F₁，F₂是双曲线

-y2=1的两个焦点，P在双曲线上，当△F₁PF₂的面积为2时，

的值为（　　）

设F₁、F₂是双曲线

=1（a＞0，b＞0）的左、右两个焦点，若双曲线右支上存在一点P，使(

=0（O为坐标原点），且tan∠PF₂F₁=2，则双曲线的离心率为（　　）