题目内容
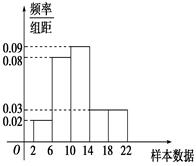
从某校参加2012年全国高中数学联赛预赛的450名同学中，随机抽取若干名同学，将他们的成绩制成频率分布表，下面给出了此表中部分数据．
（1）根据表中已知数据，你认为在①、②、③处的数值分别为 ， ， ．
（2）补全在区间 [70，140] 上的频率分布直方图；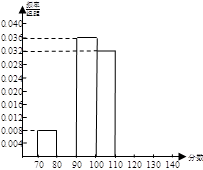
（3）若成绩不低于100分的同学能参加决赛，那么可以估计该校大约有多少学生能参加决赛？
（1）50；0.04；0.10．（2）如图．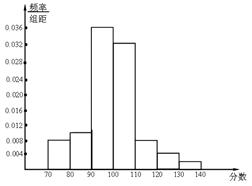 
（3）207
解析试题分析：（1）50；0.04；0.10． ……6分
（2）如图．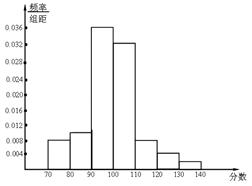 
……10分
（3）在随机抽取的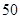
名同学中有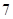
名出线,．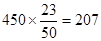
答：在参加的
名中大概有207名同学出线． ……14分
考点：本题考查了频率分布直方图的画法及运用。
点评：本题第(1)利用了频率分布表的频率之和为1，再根据比例关系即求得频数，根据此二数据即可顺利补充完整图.
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
（本题满分12分）
某车间为了规定工时定额，需要确定加共某零件所花费的时间，为此作了四次实验，得到的数据如下：
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
（2）试预测加工10个零件需要多少时间？
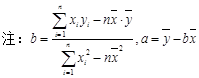
一次考试中，五名学生的数学、物理成绩如下表所示：
| 学生 | A1 | A2 | A3 | A4 | A5 |
| 数学（x分 | 89 | 91 | 93 | 95 | 97 |
| 物理（y分） | 87 | 89 | 89 | 92 | 93 |
（1）请在图的直角坐标系中作出这些数据的散点图，并求出这些数据的同归方程；
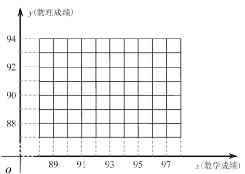
（2）要从4名数学成绩在90分以上的同学中选2人参加一项活动，以X表示选中的同学的物理成绩高于90分的人数，求随机变量X的分布列及数学期望E（X）的值．
.
，
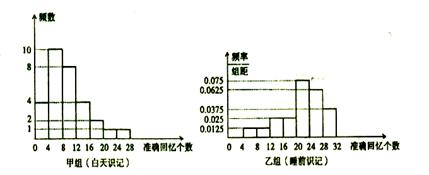
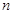值，并补全频数条形图；
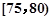，第2组
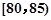，第3组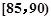
，第4组
，第5组
，得到的频率分布直方图如图所示，同时规定成绩在85分以上（含85分）的学生为“优秀”，成绩小于85分的学生为“良好”，且只有成绩为“优秀”的学生才能获得面试资格.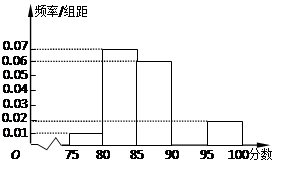
男 女
15 7 7 8 9 9 9