题目内容
【题目】某闯关游戏共有两关，游戏规则：先闯第一关，当第一关闯过后，才能进入第二关，两关都闯过，则闯关成功，且每关各有两次闯关机会.已知闯关者甲第一关每次闯过的概率均为
，第二关每次闯过的概率均为
.假设他不放弃每次闯关机会，且每次闯关互不影响.
(1)求甲恰好闯关3次才闯关成功的概率；
(2)记甲闯关的次数为
，求随机变量的分布列和期望.。
【答案】(1) 
(2)见解析
【解析】
（1）先分类，再分别根据独立事件概率乘法公式求解，最后求和得结果，（2）先确定随机变量，再分别求对应概率，列表得分布列，根据数学期望公式得结果.
解：（1）设事件
为“甲恰好闯关
次才闯关成功的概率”，则有
，
（2）由已知得：随机变量
的所有可能取值为
，
所以，
，
，
.
从而
| 2 | 3 | 4 |
|
|
|
|
.
名校课堂系列答案
【题目】新高考3+3最大的特点就是取消文理科，除语文、数学、外语之外，从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目．某研究机构为了了解学生对全理（选择物理、化学、生物）的选择是否与性别有关，觉得从某学校高一年级的650名学生中随机抽取男生，女生各25人进行模拟选科．经统计，选择全理的人数比不选全理的人数多10人．
（1）请完成下面的2×2列联表；
选择全理 | 不选择全理 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
（2）估计有多大把握认为选择全理与性别有关，并说明理由；
（3）现从这50名学生中已经选取了男生3名，女生2名进行座谈，从中抽取2名代表作问卷调查，求至少抽到一名女生的概率．
附：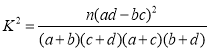
，其中
．
| 0．15 | 0．10 | 0．05 | 0．025 | 0．010 | 0．005 | 0．001 |
| 2．072 | 2．076 | 3．841 | 5．024 | 6．635 | 7．879 | 10．828 |
【题目】2019年国际篮联篮球世界杯，将于2019年在的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.为了宣传世界杯，某大学从全校学生中随机抽取了
名学生，对是否收看篮球世界杯赛事的情况进行了问卷调查，统计数据如下：
会收看 | 不会收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
（1）根据上表说明，能否有
的把握认为收看篮球世界杯赛事与性别有关？
（2）现从参与问卷调查且收看篮球世界杯赛事的学生中，采用按性别分层抽样的方法选取
人参加2019年国际篮联篮球世界杯赛志愿者宣传活动.
（i）求男、女学生各选取多少人；
（ii）若从这人中随机选取
人到校广播站开展2019年国际篮联篮球世界杯赛宣传介绍，求恰好选到名男生的概率.
附：
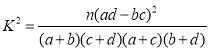，其中
.
|
|
|
|
|
|
|
|
|
|
|
|
