题目内容
【题目】已知数列{an}中,相邻两项an,an+1是关于x的方程:x2+3nx+bn![]() 0(n∈N*)的两实根,且a1=1.
0(n∈N*)的两实根,且a1=1.
(1)若Sn为数列{an}的前n项和,求S100 ;
(2)求数列{an}和{bn}的通项公式.
【答案】(1)S100=﹣7500;(2)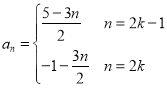 ,
,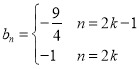
【解析】
(1)由韦达定理可得所以![]() ,即把
,即把![]() 相邻两项之和看成一个新的数列,这个新数列为等差数列,
相邻两项之和看成一个新的数列,这个新数列为等差数列,![]() 包含新数列的前50项,用等差数列的前
包含新数列的前50项,用等差数列的前![]() 项和公式即可;
项和公式即可;
(2)由![]() 、
、![]() 两式相减得
两式相减得![]() ,即隔项成等差数列,由
,即隔项成等差数列,由![]() 可得奇数项的通项,由
可得奇数项的通项,由![]() 可得偶数项的通项,由
可得偶数项的通项,由![]() 的通项可得
的通项可得![]() 的通项公式.
的通项公式.
解:(1)因为an、an+1是关于![]() 的两实根,
的两实根,
所以an+an+1=﹣3n,a2n﹣1+a2n=﹣3(2n﹣1)=3﹣6n,![]() ,
,
所以S100=﹣7500.
(2)![]() ,
,![]() ,两式相减,
,两式相减,![]() ,
,
∴![]() ,
,
因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
所以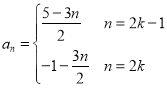 ,
,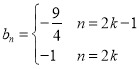 .
.

练习册系列答案
相关题目