题目内容
8. 在如图所示的多面体BACDE中,AB⊥平面ACD,DE⊥平面ACD,且AC=AD=CD=DE=2,AB=1
在如图所示的多面体BACDE中,AB⊥平面ACD,DE⊥平面ACD,且AC=AD=CD=DE=2,AB=1(1)已知M、N分别为AD、BE的中点,证明:AD⊥平面CMN;
(2)请在线段CE上找到点F的位置,使得恰有直线BF∥平面ACD,并证明这一结论.
分析 (1)先证明AD⊥CM,再结合已知证明AD⊥MN,又MN∩CM=M,即可由判定定理可证AD⊥平面MNC.
(2)分别取CE、CD的中点F、H,连接BF、FH、AH,利用三角形的中位线定理和平行四边形的判定定理及线面平行的判定定理即可证明.
解答 解:(1)∵AC=AD=CD,M为AD的中点,可得AD⊥CM,
∵AB⊥平面ACD,DE⊥平面ACD,M、N分别为AD、BE的中点,可得AD⊥MN,
又∵MN∩CM=M,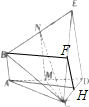
∴AD⊥平面MNC.
(2)由已知AB⊥平面ACD,DE⊥平面ACD,∴AB∥ED,
设F为线段CE的中点,H是线段CD的中点,
连接FH,则FH∥=$\frac{1}{2}$ED,∴FH∥=AB,
∴四边形ABFH是平行四边形,∴BF∥AH,
由BF?平面ACD内,AH?平面ACD,
∴BF∥平面ACD.
点评 本题主要考查了直线与平面平行的判定,直线与平面垂直的判定,解题的关键是利用三角形的中位线定理、平行四边形的判定定理及线面平行的判定定理,属于中档题.

练习册系列答案
相关题目
18. 如图是某篮球联赛中,甲、乙两名运动员9个场次得分的茎叶图,设甲、乙两人得分平均数分别为${\overline{x}}_{甲}$、${\overline{x}}_{乙}$,中位数分别为m甲,m乙,则( )
如图是某篮球联赛中,甲、乙两名运动员9个场次得分的茎叶图,设甲、乙两人得分平均数分别为${\overline{x}}_{甲}$、${\overline{x}}_{乙}$,中位数分别为m甲,m乙,则( )
 如图是某篮球联赛中,甲、乙两名运动员9个场次得分的茎叶图,设甲、乙两人得分平均数分别为${\overline{x}}_{甲}$、${\overline{x}}_{乙}$,中位数分别为m甲,m乙,则( )
如图是某篮球联赛中,甲、乙两名运动员9个场次得分的茎叶图,设甲、乙两人得分平均数分别为${\overline{x}}_{甲}$、${\overline{x}}_{乙}$,中位数分别为m甲,m乙,则( )| A. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,m甲<m乙 | B. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,m甲>m乙 | ||
| C. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,m甲>m乙 | D. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,m甲<m乙 |
20.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一个焦点F1作一条渐近线的垂线,垂足为A,与另一条渐近线交于点B,若A恰好是F1B的中点,则双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
17.已知椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)与圆C2:x2+y2=b2,若在椭圆C1上存在点P,过P作圆的切线PA,PB,切点为A,B使得∠BPA=$\frac{π}{3}$,则椭圆C1的离心率的取值范围是( )
| A. | $[\frac{{\sqrt{3}}}{2},1)$ | B. | $[\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}]$ | C. | $[\frac{{\sqrt{2}}}{2},1)$ | D. | $[\frac{1}{2},1)$ |
18.阅读下列算法:
(1)输入x.
(2)判断x>2是否成立,若是,y=x; 否则,y=-2x+6.
(3)输出y.
当输入的x∈[0,7]时,输出的y的取值范围是( )
(1)输入x.
(2)判断x>2是否成立,若是,y=x; 否则,y=-2x+6.
(3)输出y.
当输入的x∈[0,7]时,输出的y的取值范围是( )
| A. | [2,7] | B. | [2,6] | C. | [6,7] | D. | [0,7] |