题目内容
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]()
![]() ,点D在椭圆C上,
,点D在椭圆C上,![]() 的周长为
的周长为![]() .
.
(1)求椭圆C的标准方程;
(2)过圆![]() 上任意一点P作圆E的切线l,若l与椭圆C交于A,B两点,O为坐标原点,求证:
上任意一点P作圆E的切线l,若l与椭圆C交于A,B两点,O为坐标原点,求证:![]() 为定值.
为定值.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1) 由![]() ,周长
,周长![]() ,解得
,解得![]() ,
,![]() 即可求得标准方程.
即可求得标准方程.
(2)通过特殊情况![]() 的斜率不存在时,求得
的斜率不存在时,求得![]() ,再证明
,再证明![]() 的斜率存在时
的斜率存在时![]() ,即可证得
,即可证得![]() 为定值.通过设直线
为定值.通过设直线![]() 的方程为
的方程为![]() 与椭圆方程联立,借助韦达定理求得
与椭圆方程联立,借助韦达定理求得![]() ,利用直线
,利用直线![]() 与圆相切,即
与圆相切,即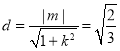 ,求得
,求得![]() 的关系代入,化简即可证得
的关系代入,化简即可证得![]() 即可证得结论.
即可证得结论.
(1)由题意得![]() ,周长
,周长![]() ,且
,且![]() .
.
联立解得![]() ,
,![]() ,所以椭圆C的标准方程为
,所以椭圆C的标准方程为![]() .
.
(2)①当直线l的斜率不存在时,不妨设其方程为![]() ,
,
则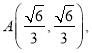
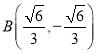 ,
,
所以![]() ,即
,即![]() .
.
②当直线l的斜率存在时,设其方程为![]() ,并设
,并设![]()
![]() ,
,
由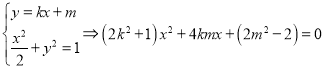 ,
,
![]() ,
,![]()
![]() ,
,
由直线l与圆E相切,得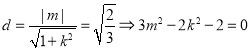 .
.
所以![]()
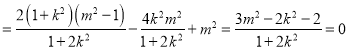 .
.
从而![]() ,即
,即![]() .
.
综合上述,得![]() 为定值.
为定值.

练习册系列答案
相关题目
【题目】某保险公司给年龄在![]() 岁的民众提供某种疾病的一年期医疗保险,现从
岁的民众提供某种疾病的一年期医疗保险,现从![]() 名参保人员中随机抽取
名参保人员中随机抽取![]() 名作为样本进行分析,按年龄段
名作为样本进行分析,按年龄段![]() 、
、![]() 、
、![]() 、
、![]() 、
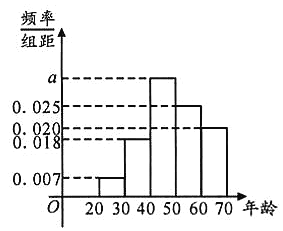
、![]() 分成了五组,其频率分布直方图如下图所示,参保年龄与每人每年应交纳的保费如下表所示.
分成了五组,其频率分布直方图如下图所示,参保年龄与每人每年应交纳的保费如下表所示.
年龄(单位:岁) |
|
|
|
|
|
保费(单位:元) |
|
|
|
|
|
(1)求频率分布直方图中实数![]() 的值,并求出该样本年龄的中位数;
的值,并求出该样本年龄的中位数;
(2)现分别在年龄段![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中各选出
中各选出![]() 人共
人共![]() 人进行回访.若从这
人进行回访.若从这![]() 人中随机选出
人中随机选出![]() 人,求这
人,求这![]() 人所交保费之和大于
人所交保费之和大于![]() 元的概率.
元的概率.