题目内容

在直角坐标系中，已知△ABC的顶点坐标为A（0，0），B（-1，2），C（0，3）．求△ABC在矩阵
0-1
10
作用下变换所得到的图形的面积．
分析：先求三角形每个点在此矩阵变换下的像的坐标，再根据坐标求变化后的三角形的面积．
解答：解：由题意，A（0，0），B（-1，2），C（0，3）在矩阵
0-1
10
作用下分别变为
D（0，0），E（-2，-1），F（-3，0）
∴所求面积为
1
2
×DE×1=
1
2
×3×1=
3
2
点评：本题主要考查矩阵的乘法及矩阵变换的性质在图形变化中的应用．考查知识点比较少有一定的计算量．
练习册系列答案
相关题目
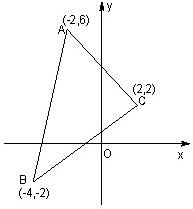精英家教网如图，在直角坐标系中，已知△ABC的三个顶点的坐标，求：
（1）直线AB的一般式方程；
（2）AC边上的高所在直线的斜截式方程．
在直角坐标系中，已知射线OA：x-y=0（x≥0），OB：x+
3
y=0（x≥0），过点P（1，0）作直线分别交射线OA，OB于A，B点．
（1）当AB中点为P时，求直线AB的方程；
（2）在（1）的条件下，若A、B两点到直线l：y=mx+2的距离相等，求实数m的值．
在直角坐标系中，已知A（cosx，sinx），B=（1，1），O为坐标原点，
OA
+
OB
=
OC
，f（x）=|
OC
|2．
（Ⅰ）求f（x）的对称中心的坐标及其在区间[-π，0]上的单调递减区间；
（Ⅱ）若f（x0）=3+
2
，x0∈[
π
2
，
3π
4
]，求tanx0的值．
（2007•普陀区一模）在直角坐标系中，已知点列P1（1，-
1
2
），P2（2，
1
22
），P3（3，-
1
23
），…，Pn（n，(-
1
2
)n），…，其中n是正整数．连接P1 P2的直线与x轴交于点X1（x1，0），连接P2 P3的直线与x轴交于点X2（x2，0），…，连接Pn Pn+1的直线与x轴交于点Xn（xn，0），…．
（1）求数列{an}的通项公式；
（2）依次记△X1P2X2的面积为S1，△X2P3X3的面积为S3，…，△XnPn+1Xn的面积为Sn，…试求无穷数列{Sn}的各项和．
精英家教网如图，在直角坐标系中，已知射线OA：x-y=0（x≥0），OB：
3
x+3y=0（x≥0），过点P（a，0）（a＞0）作直线l分别交射线OA，OB于A，B两点，且
AP
=2
PB
，则直线l的斜率为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网