题目内容
14. 如图,BC为圆O的直径,A为圆O上一点,过点A作圆O的切线交BC的延长线于点P,AH⊥PB于H.
如图,BC为圆O的直径,A为圆O上一点,过点A作圆O的切线交BC的延长线于点P,AH⊥PB于H.求证:PA•AH=PC•HB.
分析 连AC,AB,利用射影定理可得AH2=CH•HB,即$\frac{AH}{CH}=\frac{HB}{AH}$,再证明$\frac{PC}{CH}=\frac{PA}{AH}$,即$\frac{AH}{CH}=\frac{PA}{PC}$,即可得出结论.
解答 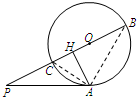 证明:连AC,AB.
证明:连AC,AB.
因BC为圆O的直径,故AC⊥AB.
又AH⊥PB,故AH2=CH•HB,即$\frac{AH}{CH}=\frac{HB}{AH}$.…5分
因PA为圆O的切线,故∠PAC=∠B.
在Rt△ABC中,∠B+∠ACB=90°.
在Rt△ACH中,∠CAH+∠ACB=90°.
所以,∠HAC=∠B.
所以,∠PAC=∠CAH,
所以,$\frac{PC}{CH}=\frac{PA}{AH}$,即$\frac{AH}{CH}=\frac{PA}{PC}$.
所以,$\frac{PA}{PC}=\frac{HB}{AH}$,即PA•AH=PC•HB.…10分.
点评 本题考查与圆有关的比例线段,考查射影定理,考查学生分析解决问题的能力,难度中等.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
19.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)与抛物线y2=8x有一个共同的焦点F,且两曲线的一个交点为P,若|PF|=5,则点F到双曲线的渐进线的距离为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{6}$ | D. | 3 |
4.已知双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b∈N*)的两个焦点F1,F2,点P是双曲线上一点,|OP|<5,|PF1|,|F1F2|,|PF2|成等比数列,则双曲线的离心率为( )
| A. | 2 | B. | 3 | C. | $\frac{5}{3}$ | D. | $\frac{\sqrt{5}}{2}$ |



