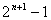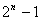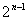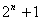题目内容
.已知数列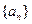 是
是 正数组成的数列,其前n项和为
正数组成的数列,其前n项和为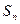 ,对于一切
,对于一切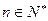 均有
均有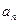 与2的等差中项等于
与2的等差中项等于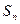 与2的等比中项。
与2的等比中项。
(1)计算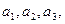 并由此猜想
并由此猜想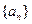 的通项公式
的通项公式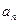 ;
;
(2)用数学归纳法证明(1)中你的猜想。
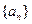 是
是 正数组成的数列,其前n项和为
正数组成的数列,其前n项和为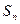 ,对于一切
,对于一切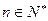 均有
均有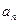 与2的等差中项等于
与2的等差中项等于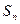 与2的等比中项。
与2的等比中项。(1)计算
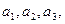 并由此猜想
并由此猜想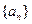 的通项公式
的通项公式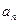 ;
;(2)用数学归纳法证明(1)中你的猜想。
解:(1)由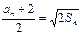 得
得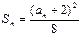 可求得
可求得 ,┈5分
,┈5分
由此猜想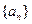 的通项公式
的通项公式 。 ┈┈┈7分
。 ┈┈┈7分
(2)证明:①当 时,
时,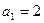 ,等式成立; ┈┈┈9分
,等式成立; ┈┈┈9分
②假设当 时,等式成立,即
时,等式成立,即 , ┈┈┈11分
, ┈┈┈11分
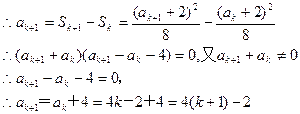
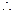 当
当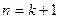 时,等式也成立
时,等式也成立 。 ┈┈┈13分
。 ┈┈┈13分
由①②可得 成立。 ┈┈┈15分
成立。 ┈┈┈15分
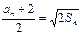 得
得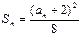 可求得
可求得 ,┈5分
,┈5分由此猜想
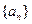 的通项公式
的通项公式 。 ┈┈┈7分
。 ┈┈┈7分(2)证明:①当
 时,
时,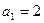 ,等式成立; ┈┈┈9分
,等式成立; ┈┈┈9分②假设当
 时,等式成立,即
时,等式成立,即 , ┈┈┈11分
, ┈┈┈11分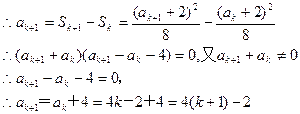
 当
当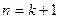 时,等式也成立
时,等式也成立 。 ┈┈┈13分
。 ┈┈┈13分由①②可得
 成立。 ┈┈┈15分
成立。 ┈┈┈15分略

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
 的最大值,求这四个数.
的最大值,求这四个数.
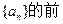 6项和为60,且
6项和为60,且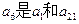 的等比中项。
的等比中项。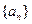 的通项公式;
的通项公式;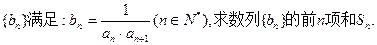
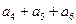 = .
= . 在等比数列
在等比数列 中,
中, ,
, ,则
,则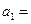 ( )
( )

 中,公比为2,前3项和为21,则
中,公比为2,前3项和为21,则 ___________
___________  的前
的前 项和为
项和为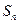 ,若
,若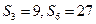 ,则
,则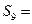 ( )
( )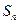 ,
,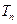 分别是首项为1的等差数列{
分别是首项为1的等差数列{ }和首项为1的等比数列{
}和首项为1的等比数列{ }的前n项和,且满足4
}的前n项和,且满足4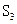 =
=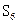 ,9
,9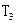 =8
=8 ,则
,则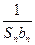 的最小值为
的最小值为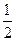


 满足
满足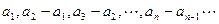 是首项为1,公比为2的等比数列,则
是首项为1,公比为2的等比数列,则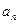 等于
等于