Question

【题目】已知数列{an}及fn（x）=a1x+a2x2+…+anxn ， fn（﹣1）=（﹣1）nn，n=1，2，3，…
（1）求a1 ， a2 ， a3的值；
（2）求数列{an}的通项公式；
（3）求证： ．

Answer 1

【答案】
（1）解：由已知f1（﹣1）=﹣a1=﹣1，所以a1=1．

f2（﹣1）=﹣a1+a2=2，所以a2=3．

f3（﹣1）=﹣a1+a2﹣a3=﹣3，所以a3=5

（2）解：令x=﹣1，则 ①

②

两式相减，得 ，

所以an+1=（n+1）+n．即an+1=2n+1．

又a1=1也满足上式，

所以数列{an}的通项公式为an=2n﹣1．（n=1，2，3…）

（3）证明： ，

所以 ．③

．④

①﹣②，得

= ，

∴ ．

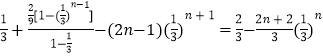又n=1，2，3…，∴ 故 ＜1．

又

∴ 是递增数列，故 …（11分）

∴

【解析】（1）由已知条件利用函数的性质能求出a1，a2，a3的值，（2）由已知条件进行错位相减能得出an+1=2n+1，进而得到数列{an}的通项公式，（3）利用错位相减法即可证明出结论.