Question

若直角坐标平面内M、N两点满足：
①点M、N都在函数f(x)的图像上；
②点M、N关于原点对称，则称这两点M、N是函数f(x)的一对“靓点”。
已知函数则函数f(x)有          对“靓点”。

Answer 1

1

本试题主要是考查了新定义的理解和运用。

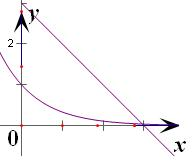
设y=x-3上任取一点M（x，y）（x＞0）
则关于原点对称的点为N（-x，-y），
根据“靓点”的定义可知点N（-x，-y）在函数f（x）的图象上，
则f（-x）=3^-x=-y
∴y=x-3，-y=3^-x，x>0即3-x=3^-x（x＞0）方程3-x=3^-x（x＞0）解的个数可看成y=3-x，y=3^-x（x＞0）的图象的交点个数，作出y=3-x，y=3^-x（x＞0）的图象可知有且只有一个交点，故函数f（x）有一对“靓点”．故答案为：1
解决该试题的关键是理解”靓点”的定义，并结合图像判定得到求解。