题目内容
已知二次函数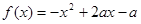 在区间
在区间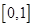 上有最大值
上有最大值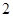 ,求实数
,求实数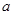 的值
的值
 或
或
解析试题分析:由已知二次函数 开口方向向下,其对称轴为
开口方向向下,其对称轴为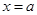 ,所以函数
,所以函数 在区间
在区间 上单调递增,在
上单调递增,在 上单调递减,又函数
上单调递减,又函数 在区间
在区间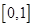 上的最大值受到
上的最大值受到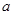 与区间端点值0、1大小关系的制约,故需要对
与区间端点值0、1大小关系的制约,故需要对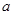 的取值范围针对于0、1进行分类讨论,即当
的取值范围针对于0、1进行分类讨论,即当 时,函数的最大值为
时,函数的最大值为 ;当
;当 时,函数的最大值为
时,函数的最大值为 ;当
;当 时,函数的最大值为
时,函数的最大值为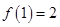 ,从而求出实数
,从而求出实数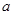 的值.
的值.
试题解析:由 ,得函数
,得函数 的对称轴为:
的对称轴为: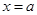 , 1分
, 1分
①当 时,
时, 在
在 上递减,
上递减, ,即
,即 ; 4分
; 4分
②当 时,
时, 在
在 上递增,
上递增, ,即
,即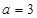 ; 7分
; 7分
③当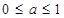 时,
时, 在
在 递增,在
递增,在 上递减,
上递减,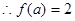 ,即
,即 ,解得:
,解得: 与
与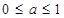 矛盾;
矛盾;
综上:a =-2或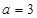 10分
10分
考点:二次函数的最值

练习册系列答案
相关题目
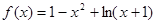
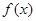 的单调区间;
的单调区间;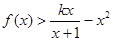 (
(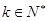 )在
)在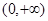 上恒成立,求
上恒成立,求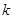 的最大值.
的最大值. .
.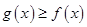 ,求实数x的取值范围;
,求实数x的取值范围; 的最大值.
的最大值. .
. 时,函数最大值为2,求
时,函数最大值为2,求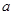 的值.
的值. 为奇函数.
为奇函数.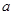 的值;
的值; 的图象由函数
的图象由函数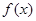 的图象先向右平移2个单位,再向上平移2个单位得到,写出
的图象先向右平移2个单位,再向上平移2个单位得到,写出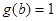 ,求
,求 的值.
的值.
 的定义域;
的定义域; 的值;
的值; )升,司机的工资是每小时14元.
)升,司机的工资是每小时14元. .
.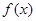 为奇函数,求实数
为奇函数,求实数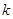 的值;
的值;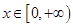 ,都有
,都有 成立,求实数
成立,求实数 。
。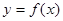 的定义域;
的定义域; 的值,作出函数
的值,作出函数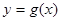 的图象并指出函数
的图象并指出函数