题目内容
【题目】关于函数，给出下列命题：
①若函数f(x)是R上周期为3的偶函数，且满足f(1)＝1，则f(2)－f(－4)＝0；
②若函数f(x)满足f(x＋1)f(x)＝2 017，则f(x)是周期函数；
③若函数g(x)＝
是偶函数，则f(x)＝x＋1；
④函数y＝
的定义域为
.
其中正确的命题是________.(写出所有正确命题的序号)
【答案】①②
【解析】①因为f(x＋3)＝f(x)且f(－x)＝f(x)，所以f(2)＝f(－1＋3)＝f(－1)＝f(1)＝1，f(－4)＝f(－1)＝f(1)＝1，故f(2)－f(－4)＝0，①正确.
②因为f(x＋1)f(x)＝2 017，所以f(x＋1)＝
，f(x＋2)＝
＝f(x).所以f(x)是周期为2的周期函数，②正确.
③令x＜0，则－x＞0，g(－x)＝－x－1.又g(x)为偶函数，所以g(x)＝g(－x)＝－x－1.即f(x)＝－x－1，③不正确.
④要使函数有意义，需满足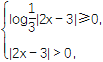
即0＜|2x－3|≤1，
所以1≤x≤2且x≠
，即函数的定义域为
∪
，④不正确.
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
