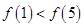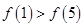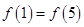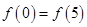题目内容
奇函数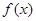 在区间
在区间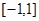 上是增函数,且
上是增函数,且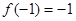 ,当
,当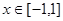 时,函数
时,函数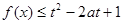 对一切
对一切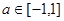 恒成立,则实数
恒成立,则实数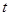 的取值范围是 ( )
的取值范围是 ( )
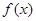 在区间
在区间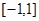 上是增函数,且
上是增函数,且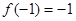 ,当
,当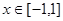 时,函数
时,函数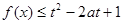 对一切
对一切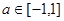 恒成立,则实数
恒成立,则实数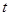 的取值范围是 ( )
的取值范围是 ( )A.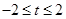 | B.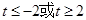 |
C.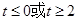 | D.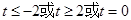 |
D
试题分析:奇函数f(x)在[-1,1]上是增函数,且f(-1)=-1,在[-1,1]最大值是1,∴1≤t2-2at+1,当t=0时显然成立,当t≠0时,则t2-2at≥0成立,又a∈[-1,1],令g(a)=2at-t2,a∈[-1,1],当t>0时,g(a)是减函数,故令g(1)≥0,解得t≥2,当t<0时,g(a)是增函数,故令g(-1)≥0,解得t≤-2,综上知,t≥2或t≤-2或t=0.选D.

练习册系列答案
相关题目
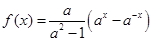 ,其中
,其中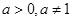
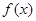 ,当
,当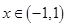 时,
时,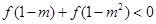 ,求实数
,求实数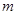 的取值集合;
的取值集合;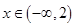 时,
时,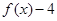 的值为负,求
的值为负,求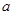 的取值范围.
的取值范围.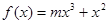 为偶函数,则实数
为偶函数,则实数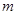 的值为__________.
的值为__________.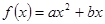 是定义在
是定义在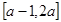 上的偶函数,那么
上的偶函数,那么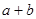 =
= 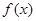 是
是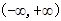 上的奇函数,且
上的奇函数,且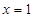 对称,当
对称,当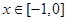 时,
时, ,则
,则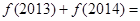 .
.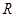 上的偶函数
上的偶函数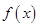 满足
满足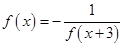 且
且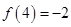 ,则
,则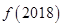 的值为( )
的值为( )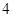
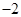
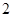
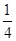
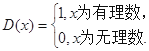 ,则D(x) ( )
,则D(x) ( )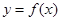 满足条件
满足条件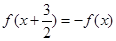 ,且
,且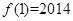 ,则
,则 .
.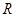 上的函数
上的函数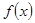 在区间
在区间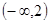 上是增函数,且
上是增函数,且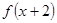 的图象关于
的图象关于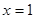 对称,则( )
对称,则( )