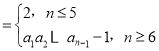Question

【题目】已知函数.

（Ⅰ）若，函数在区间上有意义且不单调，求a的取值范围；

（Ⅱ）若，且，求a的取值范围．

Answer 1

【答案】（Ⅰ）﹣6＜a＜﹣2；（Ⅱ）0≤a．

【解析】

（Ⅰ）当时，，由题知：二次函数f（x）的对称轴在（1，4）之间，且f（x）在[1，4]上恒为正，列出不等式组，即可求出a的取值范围；

（Ⅱ）因为，设m，n（m≤n）为方程f（x）＝1的两个根，所以，

由，解得a≥0或a≤﹣4，又m，n（m≤n）为方程f（x）＝1的两个根，所以m＝﹣1﹣a，即可求出a的取值范围．

解：（Ⅰ）当时，，

由题知：二次函数的对称轴在之间，且在上恒为正，

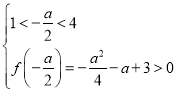∴，解得：；

（Ⅱ）因为，设m，n（m≤n）为方程的两个根，

∴，

由，得n﹣1＝0且，由得，所以，

因为，

∴，解得或，

又m，n（m≤n）为方程的两个根，所以，

∴，解得，

综上所述：．