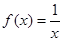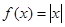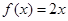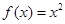题目内容
设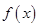 定义在R且x不为零的偶函数,在区间
定义在R且x不为零的偶函数,在区间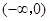 上递增, f(xy)=f(x)+f(y),当a满足
上递增, f(xy)=f(x)+f(y),当a满足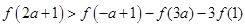 则a的取值范围是( )。
则a的取值范围是( )。
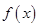 定义在R且x不为零的偶函数,在区间
定义在R且x不为零的偶函数,在区间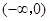 上递增, f(xy)=f(x)+f(y),当a满足
上递增, f(xy)=f(x)+f(y),当a满足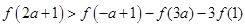 则a的取值范围是( )。
则a的取值范围是( )。A.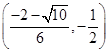 |
B.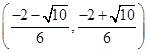 |
C.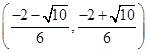 且a 且a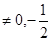 |
D.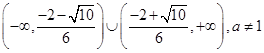 |
C
解:由f(xy)=f(x)+f(y)?f(1×1)=f(1)+f(1)?f(1)=0;
∴f(2a+1)>f(-a+1)-f(3a)-3f(1)
?f(2a+1)+f(3a)>f(-a+1)
?f[(2a+1)3a]>f(-a+1);①
∵f(x)定义在R且x不为零的偶函数;
∴①转化为f(|3a(2a+1)|)>f(|-a+1|)②
∵函数在区间(-∞,0)上递增,
∴函数在区间(0,+∞)上递增,
∴②转化为|3a(2a+1)|<|-a+1|?[3a(2a+1)]2<(-a+1)2?[3a(2a+1)-(-a+1)][3a(2a+1)+(-a+1)]<0?(6a2+2a+1)(6a2+4a-1)<0;
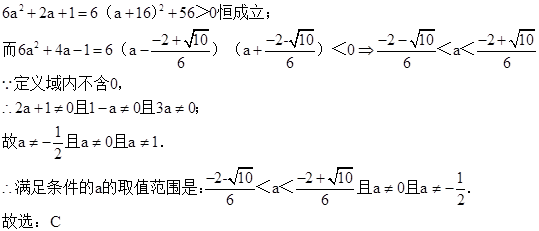

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
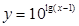 的图象相同的函数是 ( )
的图象相同的函数是 ( )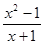
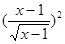
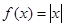 与
与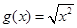
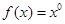 与
与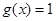
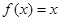 与
与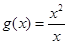
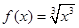 与
与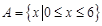 ,
,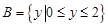 ,从
,从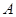 到
到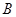 的对应法则
的对应法则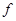 不是映射的是( )
不是映射的是( )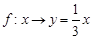 B.
B.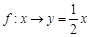 C.
C.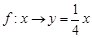 D.
D.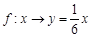
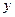 =
=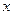 +
+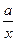 有如下性质:如果常数
有如下性质:如果常数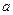 >0,那么该
>0,那么该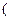 0,
0,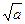
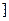 上是减函数,在
上是减函数,在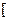
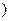 上是增函数.
上是增函数.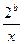 (
(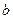 的值;
的值;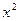 +
+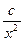 (常数
(常数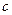 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;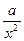 (常数
(常数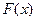 =
=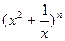 +
+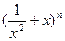 (
(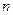 是正整数)在区间[
是正整数)在区间[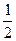 ,2]上的最大值和最小值(可利用你
,2]上的最大值和最小值(可利用你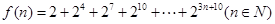 ,则
,则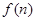 等于( )
等于( )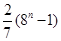
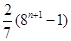
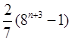
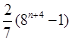
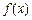 是定义在R上的
是定义在R上的 函数,
函数,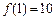 ,且对于任意
,且对于任意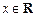 都有
都有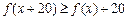 ,
,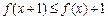 ,若
,若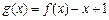 ,则
,则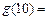 _____________.
_____________.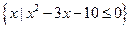 ,B={
,B={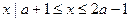 },若B
},若B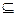 A,则-3
A,则-3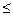 a
a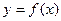 与直线x=l的交点个数为0或l;
与直线x=l的交点个数为0或l;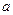
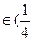 ,+∞)时,函数
,+∞)时,函数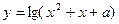
 的值域为R;
的值域为R;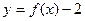 关于点(1,-1)对称的函数为
关于点(1,-1)对称的函数为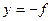 (2 -x
(2 -x ).
).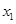 ,
,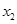 (
(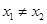 ).
). 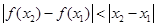 恒成立”的只有( )
恒成立”的只有( )