题目内容
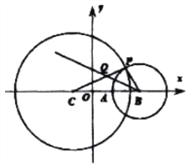
【题目】如图,在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
: ![]() ,点
,点![]() ,点
,点![]() (
(![]() ),以
),以![]() 为圆心,
为圆心, ![]() 为半径作圆,交圆
为半径作圆,交圆![]() 于点
于点![]() ,且
,且![]() 的平分线交线段
的平分线交线段![]() 于点
于点![]() .
.
(1)当![]() 变化时,点
变化时,点![]() 始终在某圆锥曲线
始终在某圆锥曲线![]() 上运动,求曲线
上运动,求曲线![]() 的方程;
的方程;
(2)已知直线![]() 过点
过点 ![]() ,且与曲线
,且与曲线![]() 交于
交于 ![]() 两点,记
两点,记![]() 面积为
面积为![]() ,
, ![]() 面积为
面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(I)推导出△QAB≌△QPB,从而QC+QA=4,由椭圆的定义可知,Q点的轨迹是以C,A为焦点, ![]() 的椭圆,由此能求出点Q的轨迹方程.
的椭圆,由此能求出点Q的轨迹方程.
(II)设直线l:x=my-1,设M(x1,y1),N(x2,y2),推导出![]() ,由
,由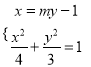 得
得![]() ,由此利用根的判别式、韦达定理,结合已知条件求出
,由此利用根的判别式、韦达定理,结合已知条件求出![]() 的取值范围.
的取值范围.
试题解析:
(1)∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ≌
≌![]() ,∴
,∴![]() ,
,
∵![]() ,
,
由椭圆的定义可知, ![]() 点的轨迹是以
点的轨迹是以![]() ,
, ![]() 为焦点,
为焦点, ![]() 的椭圆,
的椭圆,
故点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)由题可知,设直线 ![]() :
: ![]() ,不妨设
,不妨设 ![]() ,
, ![]()
∵![]()
![]() ,
,
∵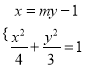 ,∴
,∴![]() ,
, ![]() ,
,
∴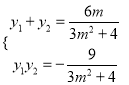 ,
,
∵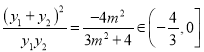 ,即
,即![]() ,
,
∴![]() ,
,
∴![]()
![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
