题目内容
【题目】设△ABC的内角A,B,C所对的边长分别为a,b,c,且满足a2+c2-b2=![]() ac.
ac.
(1)求角B的大小;
(2)若2bcos A=![]() (ccosA+acosC),BC边上的中线AM的长为
(ccosA+acosC),BC边上的中线AM的长为![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:![]() 利用余弦定理表示出
利用余弦定理表示出![]() ,将已知等式变形后代入求出
,将已知等式变形后代入求出![]() 的值,由
的值,由![]() 为三角形内角,利用特殊角的三角函数值就可求出
为三角形内角,利用特殊角的三角函数值就可求出![]() 的大小;
的大小;
![]() 利用正弦定理化简已知等式,求出
利用正弦定理化简已知等式,求出![]() 的值,由
的值,由![]() 为三角形内角,利用特殊角的三角函数值求出
为三角形内角,利用特殊角的三角函数值求出![]() 的大小,确定出
的大小,确定出![]() 的大小,设
的大小,设![]() ,利用余弦定理列出关于
,利用余弦定理列出关于![]() 的方程,求出方程的解得到
的方程,求出方程的解得到![]() 的值,确定出
的值,确定出![]() 和
和![]() ,即可求出
,即可求出![]() 的面积。
的面积。
解析:(1)由余弦定理,得cosB=![]() =
=![]() =
=![]() .
.
因为B是三角形的内角,所以B=![]() .
.
(2)由正弦定理,得![]() =
=![]() =
=![]() ,
,
代入2bcos A=![]() (ccosA+acosC),
(ccosA+acosC),
可得2sin BcosA=![]() (sin CcosA+sin AcosC),
(sin CcosA+sin AcosC),
即2sin BcosA=![]() sin B.
sin B.
因为B∈(0,π),所以sin B≠0,
所以cosA=![]() ,
,
所以A=![]() ,则C=π-A-B=
,则C=π-A-B=![]() .
.
设AC=m(m>0),则BC=m,
所以CM=![]() m.
m.
在△AMC中,由余弦定理,得
AM2=CM2+AC2-2CM·AC·cos![]() ,
,
即(![]() )2=
)2=![]() m2+m2-2·
m2+m2-2·![]() m·m·(-
m·m·(-![]() ),整理得m2=4,解得m=2.
),整理得m2=4,解得m=2.
所以S△ABC=![]() CA·CBsin
CA·CBsin![]() =
=![]() ×2×2×
×2×2×![]() =
=![]() .
.

【题目】学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如表:
损坏餐椅数 | 未损坏餐椅数 | 总计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总计 | 80 | 320 | 400 |
![]() 求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
![]() 请说明是否有
请说明是否有![]() 以上的把握认为损毁餐椅数量与学习雷锋精神
以上的把握认为损毁餐椅数量与学习雷锋精神
有关?![]() 参考公式:
参考公式:![]() ,
,
|
|
|
|
|
|
|
|
|
|
|
|
【题目】某面包店随机收集了面包种类的有关数据,经分类整理得到下表:
面包类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
面包个数 | 90 | 60 | 30 | 80 | 100 | 40 |
好评率 | 0.6 | 0.45 | 0.7 | 0.35 | 0.6 | 0.5 |
好评率是指:一类面包中获得好评的个数与该类面包的个数的比值.
(1)从面包店收集的面包中随机选取1个,求这个面包是获得好评的第五类面包的概率;
(2)从面包店收集的面包中随机选取1个,估计这个面包没有获得好评的概率;
(3)面包店为增加利润,拟改变生产策略,这将导致不同类型面包的好评率发生变化.假设表格中只有两类面包的好评率数据发生变化,那么哪类面包的好评率增加0.1,哪类面包的好评率减少0.1,使得获得好评的面包总数与样本中的面包总数的比值达到最大?(只需写出结论)
【题目】2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,并作出如图频率分布直方图:
五组,并作出如图频率分布直方图:
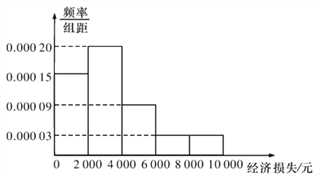
(1)试根据频率分布直方图估计小区平均每户居民的平均损失(同一组中的数据用该组区间的中点值代表);
(2)小明向班级同学发出倡议,为该小区居民捐款,现从损失超过4000元的居民中随机抽取2户进行捐款援助,设抽出损失超过8000元的居民为![]() 户,求
户,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如图,根据图表格中所给数据,分别求![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值,并说明是否有
的值,并说明是否有![]() 以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
捐款超过500元 |
|
| |
捐款不超过500元 |
|
| |
合计 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附:临界值表参考公式:![]() ,
,![]() .
.