题目内容
(Ⅰ)30°(Ⅱ)
解析试题分析:(Ⅰ) 延长AD,FE交于Q.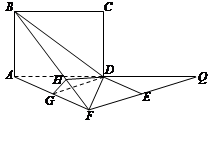
因为ABCD是矩形,所以
BC∥AD,
所以∠AQF是异面直线EF与BC所成的角.
在梯形ADEF中,因为DE∥AF,AF⊥FE,AF=2,DE=1得
∠AQF=30°.
(Ⅱ) 方法一:
设AB=x.取AF的中点G.由题意得
DG⊥AF.
因为平面ABCD⊥平面ADEF,AB⊥AD,所以
AB⊥平面ADEF,
所以
AB⊥DG.
所以
DG⊥平面ABF.
过G作GH⊥BF,垂足为H,连结DH,则DH⊥BF,
所以∠DHG为二面角A-BF-D的平面角.
在直角△AGD中,AD=2,AG=1,得
DG= .
.
在直角△BAF中,由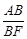 =sin∠AFB=
=sin∠AFB=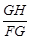 ,得
,得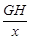 =
=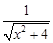 ,
,
所以
GH=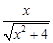 .
.
在直角△DGH中,DG= ,GH=
,GH=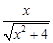 ,得
,得
DH=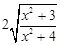 .
.
因为cos∠DHG=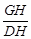 =
=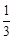 ,得
,得
x= ,
,
所以 AB= .
.
方法二:设AB=x.
以F为原点,AF,FQ所在的直线分别为x轴,y轴建立空间直角坐标系Fxyz.则
F(0,0,0),A(-2,0,0),E( ,0,0),D(-1,
,0,0),D(-1, ,0),B(-2,0,x),
,0),B(-2,0,x),
所以 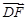 =(1,-
=(1,- ,0),
,0), =(2,0,-x).
=(2,0,-x).
因为EF⊥平面ABF,所以平面ABF的法向量可取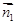 =(0,1,0).
=(0,1,0).
设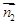 =(x1,y1,z1)为平面BFD的法向量,则
=(x1,y1,z1)为平面BFD的法向量,则 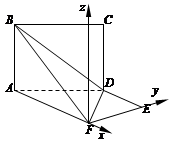
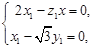
所以,可取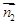 =(
=( ,1,
,1, ).
).
因为cos<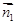 ,
,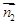 >=
>=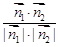 =
=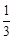 ,得
,得
x= ,
,
所以
AB= .
.
考点:异面直线所成角 二面角
点评:本题主要考查空间点、线、面位置关系,异面直线所成角、二面角等基础知识,空间向量的应用,同时考查空间想象能力和运算求解能力。

练习册系列答案
相关题目
 平面ABC,
平面ABC,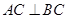 ,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。
,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。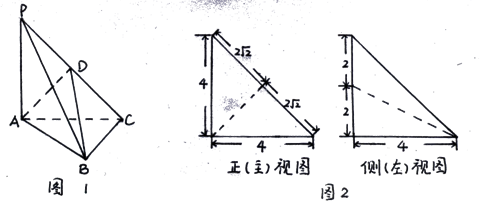
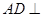 平面PBC;
平面PBC; 的平分线上确定一点Q,使得
的平分线上确定一点Q,使得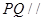 平面ABD,并求此时PQ的长。
平面ABD,并求此时PQ的长。 底面ABCD,E是PC的中点.
底面ABCD,E是PC的中点.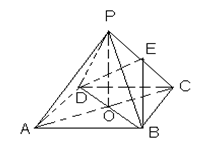
 中,底面
中,底面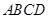 是直角梯形,AB∥CD,∠ABC=
是直角梯形,AB∥CD,∠ABC=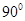 ,AB=PB=PC=BC=2CD=2,平面PBC⊥平面ABCD
,AB=PB=PC=BC=2CD=2,平面PBC⊥平面ABCD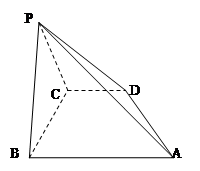
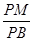 的值。若不存在,请说明理由。
的值。若不存在,请说明理由。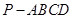 中,
中,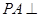 底面
底面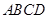 ,
,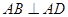 ,
, ,
,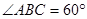 ,
,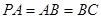 ,
, 是
是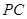 的中点。
的中点。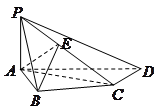
 ;
;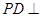 平面
平面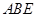 ;
;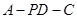 的正切值.
的正切值.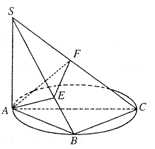
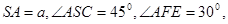 求三棱锥S—AEF的体积.
求三棱锥S—AEF的体积.
 中,
中,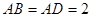 ,
,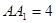 ,点
,点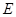 在
在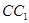 上,且
上,且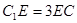 .
.
 平面
平面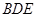 ;
;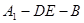 的余弦值.
的余弦值.