题目内容
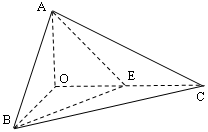
(本小题满分12分)在几何体ABCDE中,∠BAC=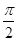 ,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1
,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1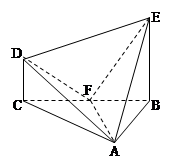
(Ⅰ)求证:DC∥平面ABE;
(Ⅱ)求证:AF⊥平面BCDE;
(Ⅲ)求证:平面AFD⊥平面AFE.
(Ⅰ) 先证DC//EB,再推出DC∥平面ABE;
(Ⅱ)证DC⊥AF,进一步AF⊥平面BCDE。
(Ⅲ)由(2)推出AF⊥EF,在直角梯形BCDE中,计算DF=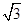 ,EF=
,EF= ,DE=
,DE=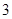
证明EF⊥平面AFD,推出平面AFD⊥平面AFE.
解析试题分析:(Ⅰ) ∵DC⊥平面ABC,EB⊥平面ABC
∴DC//EB,
又∵DC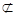 平面ABE,EB
平面ABE,EB 平面ABE,
平面ABE,
∴DC∥平面ABE………………………………………………(4分)
(Ⅱ)∵DC⊥平面ABC,
∴DC⊥AF,
又∵AF⊥BC,DC交BC于C
∴AF⊥平面BCDE……………………………………(8分)
(Ⅲ)由(2)知AF⊥平面BCDE,
∴AF⊥EF,在直角梯形BCDE中,计算DF=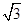 ,EF=
,EF= ,DE=
,DE=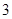
在三角形DEF中DF⊥EF,AF⊥EF,DF交AF于F
∴EF⊥平面AFD,又EF 平面AFE,
平面AFE,
∴平面AFD⊥平面AFE.…………………………………………(12分)
考点:本题主要考查立体几何中线面平行与垂直的证明。
点评:典型题,立体几何中平行、垂直关系的证明及角的计算问题是高考中的必考题,本题难度不大,注意牢记定理巧妙地实现线线关系、线面关系及面面关系的相互转化。

练习册系列答案
相关题目

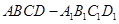 是正方体,其中
是正方体,其中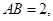
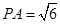
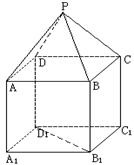
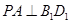 ;
;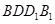 所成的锐二面角
所成的锐二面角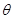 的余弦值;
的余弦值;

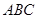 为底面的直棱柱被平面
为底面的直棱柱被平面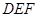 所截而得.
所截而得. 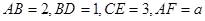 ,
, 为
为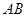 的中点.
的中点.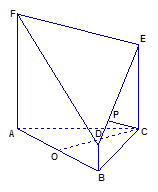
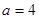 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱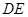 上存在点
上存在点 ,使
,使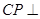 平面
平面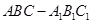 中,
中,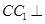 平面
平面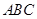 ,
,  ,点
,点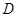 是
是 的中点.
的中点.
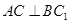 ;(2)
;(2)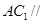 平面
平面 .
.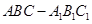 的侧面
的侧面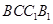 是菱形,
是菱形,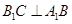
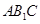
 平面
平面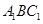 ;
; 是
是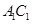 上的点,且
上的点,且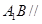 平面
平面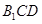 ,求
,求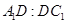 的值.
的值.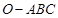 的侧棱
的侧棱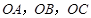 两两垂直,
两两垂直,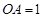 ,
, ,
,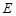 是
是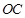 的中点。
的中点。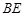 与
与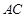 所成角的余弦值;
所成角的余弦值;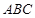 的所成角的正弦值。
的所成角的正弦值。